题目内容
5.某超市购进一批单价为28元的日用品,如果按每件40元的价格销售,每月能卖200件,根据销售统计,每件日用品的售价每降价1元,每月可多售出25件.(Ⅰ)写出该日用品每月的销售利润y元与售价x元之间的函数关系式;
(Ⅱ)求出售价为多少元时,该日用品每月的销售利润最大?最大利润是多少?
分析 (1)根据利润=(售价-成本)×售出件数,即可得到y元与售价x元之间的函数关系式;
(2)根据利润的函数解析式,利用顶点坐标公式解决问题.
解答 解:(1)销售利润y=(x-28)[25×(40-x)+200]=-25x2+1900x-33600;
(2)∵y=-25x2+1900x-33600;
∴当x=38时,W最大值=2500(元).
答:售价为38元时,该日用品每月的销售最大利润是2500元.
点评 本题主要考查了二次函数的应用的知识点,解答本题的关键熟练掌握二次函数的性质以及二次函数最大值的求解.

练习册系列答案
相关题目
20.一件商品的原价是118元,经过两次提价后的价格为168元.如果每次提价的百分率都是x,根据题意,下面列出的方程正确的是( )
| A. | 118(1+x)=168 | B. | 118(1+2x)=168 | C. | 118(1-x)2=168 | D. | 118(1+x)2=168 |
17.已知线段AB=5cm,BC=3cm,则线段AC的长度是( )
| A. | 8cm | B. | 2cm | C. | 8cm或2cm | D. | 无法确定 |
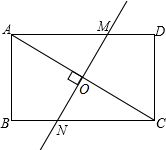 如图,在矩形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于N,交BC于M,交AC于O.
如图,在矩形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于N,交BC于M,交AC于O. 如图,△ABC中,点D、E分别在AB、AC上,且DE∥BC,若S△ADE=4,S△BDE=3,那么DE:BC=4:7.
如图,△ABC中,点D、E分别在AB、AC上,且DE∥BC,若S△ADE=4,S△BDE=3,那么DE:BC=4:7.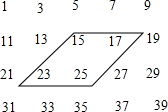 如图所示的数据是小明同学用一些奇数排成的,你能与小明一起探讨下列问题吗?动手试一试
如图所示的数据是小明同学用一些奇数排成的,你能与小明一起探讨下列问题吗?动手试一试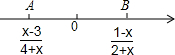 如图,点A,B在数轴上,它们所对应的数分别是$\frac{x-3}{4+x}$和$\frac{1-x}{2+x}$,且点A,B到原点的距离相等,求点A,B对应的数分别是多少?
如图,点A,B在数轴上,它们所对应的数分别是$\frac{x-3}{4+x}$和$\frac{1-x}{2+x}$,且点A,B到原点的距离相等,求点A,B对应的数分别是多少?