题目内容
15.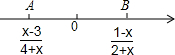 如图,点A,B在数轴上,它们所对应的数分别是$\frac{x-3}{4+x}$和$\frac{1-x}{2+x}$,且点A,B到原点的距离相等,求点A,B对应的数分别是多少?
如图,点A,B在数轴上,它们所对应的数分别是$\frac{x-3}{4+x}$和$\frac{1-x}{2+x}$,且点A,B到原点的距离相等,求点A,B对应的数分别是多少?
分析 根据点A,B在数轴上,它们所对应的数分别是$\frac{x-3}{4+x}$和$\frac{1-x}{2+x}$,且点A,B到原点的距离相等,可知$\frac{x-3}{4+x}$与$\frac{1-x}{2+x}$互为相反数,从而可以求得点A,B对应的数.
解答 解:∵点A,B在数轴上,它们所对应的数分别是$\frac{x-3}{4+x}$和$\frac{1-x}{2+x}$,且点A,B到原点的距离相等,
∴$\frac{x-3}{4+x}$+$\frac{1-x}{2+x}$=0.
解得x=-0.5.
∴$\frac{x-3}{4+x}=\frac{-0.5-3}{4+(-0.5)}=\frac{-3.5}{3.5}=-1$,$\frac{1-x}{2+x}=\frac{1-(-0.5)}{2+(-0.5)}=\frac{1.5}{1.5}=1$.
∴点A,B对应的数分别是-1,1.
点评 本题考查解分式方程、实数与数轴,解题的关键是明确到原点的距离相等的两点对应的数的绝对值相等,在原点两侧,则这两个数互为相反数.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
10. 如图,C、D是线段AB上的两点,且D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长为( )
如图,C、D是线段AB上的两点,且D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长为( )
 如图,C、D是线段AB上的两点,且D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长为( )
如图,C、D是线段AB上的两点,且D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 6cm |
20.下列条件中,不能得到等边三角形的是( )
| A. | 有两个角是60°的三角形 | B. | 有一个角是60°的等腰三角形 | ||
| C. | 有两个外角相等的等腰三角形 | D. | 三边都相等的三角形 |
 如图,在矩形ABCD中,两对角线相交于点O,AO=4cm,AB=6cm,求sin∠CAB和sin∠CBD的值.
如图,在矩形ABCD中,两对角线相交于点O,AO=4cm,AB=6cm,求sin∠CAB和sin∠CBD的值.