题目内容
15.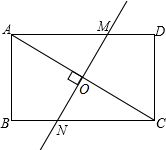 如图,在矩形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于N,交BC于M,交AC于O.
如图,在矩形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于N,交BC于M,交AC于O.(1)求证:△COM∽△ADC;
(2)求线段OM的长度.
分析 (1)首先由矩形的性质和垂直平分线的性质得∠D=∠MOC=90°,∠DAC=∠OCM,得到结论;
(2)由勾股定理可得AC的长,易得OC的长,再由△COM∽△ADC,利用相似三角形的性质可得$\frac{OM}{CD}=\frac{OC}{AD}$,代入得出结果.
解答 (1)证明:∵四边形ABCD是矩形,
∴∠D=90°,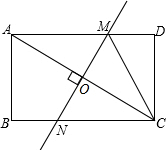
∵MN是线段AC的垂直平分线,
∴∠MOC=90°,AM=CM,
∴∠MAC=∠MCA,
即∠DAC=∠OCM,
∵∠D=∠MOC=90°,
∴△COM∽△ADC;
(2)解:∵四边形ABCD是矩形
∴AD=BC=8,CD=AD=6,∠B=90°,
∴AC=$\sqrt{{AB}^{2}{+BC}^{2}}$=$\sqrt{{6}^{2}{+8}^{2}}$=10,
∵MN是线段AC的垂直平分线
∴OA=OC=$\frac{1}{2}$AC=5,
∵△COM∽△ADC,
∴$\frac{OM}{CD}=\frac{OC}{AD}$,
即:$\frac{OM}{6}$=$\frac{5}{8}$,
∴OM=$\frac{15}{4}$.
点评 本题主要考查了相似三角形的性质及判定定理,综合运用相似三角形的性质和判定定理是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.在代数式$\frac{2}{3}$x,$\frac{3x}{x+4}$,$\frac{3{x}^{2}-5}{2x}$,2-$\frac{1}{x}$,$\frac{{x}^{2}}{x}$,$\frac{1}{π}$中,其中分式共有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
20.实数9的平方根是( )
| A. | ±3 | B. | 3 | C. | ±$\sqrt{3}$ | D. | $\sqrt{3}$ |
 如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A,B两点间的距离为10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A,B两点间的距离为10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.