题目内容
 如图,在平行四边形ABCD中,点O为对角线AC的中点,EF过点O且垂直于AC,则四边形AFCE是菱形吗?请说出理由.
如图,在平行四边形ABCD中,点O为对角线AC的中点,EF过点O且垂直于AC,则四边形AFCE是菱形吗?请说出理由.考点:菱形的判定
专题:
分析:首先得出△AOE≌△COF(ASA),则AE=CF,进而求出四边形AFCE是平行四边形,再利用EF过点O且垂直于AC,得出即可.
解答:解:四边形AFCE是菱形,理由如下:
∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAC=∠BCA
又∵点O为对角线AC的中点,∴AO=CO,
在△AOE和△COF中,
,
∴△AOE≌△COF(ASA),
∴AE=CF
∴四边形AFCE是平行四边形
∵EF⊥AC,
∴四边形AFCE是菱形.
∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAC=∠BCA
又∵点O为对角线AC的中点,∴AO=CO,
在△AOE和△COF中,
|
∴△AOE≌△COF(ASA),
∴AE=CF
∴四边形AFCE是平行四边形
∵EF⊥AC,
∴四边形AFCE是菱形.
点评:此题主要考查了菱形的判定以及全等三角形的判定与性质,得出△AOE≌△COF是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,⊙O的直径AB垂直弦CD于点P,且点P的半径OB的中点,CD=2
如图,⊙O的直径AB垂直弦CD于点P,且点P的半径OB的中点,CD=2| 3 |
A、
| ||
| B、2cm | ||
| C、4cm | ||
D、2
|
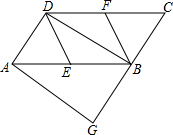 如图,在?ABCD中,∠DAB=60°,AB=2AD,点E是AB的中点,过点A作AG∥BD,交CB的延长线于点G.请判断四边形AGBD是什么特殊四边形?并加以证明.
如图,在?ABCD中,∠DAB=60°,AB=2AD,点E是AB的中点,过点A作AG∥BD,交CB的延长线于点G.请判断四边形AGBD是什么特殊四边形?并加以证明.