题目内容
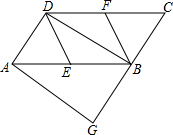 如图,在?ABCD中,∠DAB=60°,AB=2AD,点E是AB的中点,过点A作AG∥BD,交CB的延长线于点G.请判断四边形AGBD是什么特殊四边形?并加以证明.
如图,在?ABCD中,∠DAB=60°,AB=2AD,点E是AB的中点,过点A作AG∥BD,交CB的延长线于点G.请判断四边形AGBD是什么特殊四边形?并加以证明.考点:矩形的判定,平行四边形的性质
专题:
分析:根据已知推出△ADE是等边三角形,推出AE=DE=BE,推出∠ADB是直角,根据矩形的判定推出即可.
解答:答:四边形AGBD是矩形.
证明:∵∠DAB=60°,AB=2AD,点E是AB的中点,
∴AD=AE,
∴△ADE是等边三角形,
∴DE=AE=BE,
∴AD⊥BD,
∴∠ADB=90°,
∵AG∥BD
∴AD⊥AG
∴四边形AGBD是矩形.
证明:∵∠DAB=60°,AB=2AD,点E是AB的中点,
∴AD=AE,
∴△ADE是等边三角形,
∴DE=AE=BE,
∴AD⊥BD,
∴∠ADB=90°,
∵AG∥BD
∴AD⊥AG
∴四边形AGBD是矩形.
点评:本题考查了平行四边形的性质,矩形的判定,等边三角形的性质和判定的应用,解此题的关键是推出∠ADB=90°,注意:有一个角是直角的平行四边形是矩形.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
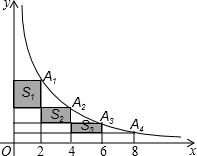 在反比例函数y=
在反比例函数y= 如图,在平行四边形ABCD中,点O为对角线AC的中点,EF过点O且垂直于AC,则四边形AFCE是菱形吗?请说出理由.
如图,在平行四边形ABCD中,点O为对角线AC的中点,EF过点O且垂直于AC,则四边形AFCE是菱形吗?请说出理由.