题目内容
 如图,⊙O的直径AB垂直弦CD于点P,且点P的半径OB的中点,CD=2
如图,⊙O的直径AB垂直弦CD于点P,且点P的半径OB的中点,CD=2| 3 |
A、
| ||
| B、2cm | ||
| C、4cm | ||
D、2
|
考点:垂径定理,勾股定理
专题:
分析:连接OD,设⊙O的半径为R,则OP=
R,根据垂径定理求出DP=CP=
cm,在Rt△OPD中,由勾股定理得出方程R2=(
R)2+(
)2,求出R即可.
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
解答: 解:连接OD,设⊙O的半径为R,
解:连接OD,设⊙O的半径为R,
则OP=
R,
∵AB⊥CD,CD=2
cm,
∴DP=CP=
cm,
在Rt△OPD中,由勾股定理得:OD2=OP2+DP2,
R2=(
R)2+(
)2,
解得:R=2,
即⊙O的直径AB=4cm,
故选C.
 解:连接OD,设⊙O的半径为R,
解:连接OD,设⊙O的半径为R,则OP=
| 1 |
| 2 |
∵AB⊥CD,CD=2
| 3 |
∴DP=CP=
| 3 |
在Rt△OPD中,由勾股定理得:OD2=OP2+DP2,
R2=(
| 1 |
| 2 |
| 3 |
解得:R=2,
即⊙O的直径AB=4cm,
故选C.
点评:本题考查了垂径定理,勾股定理得应用,解此题的关键是能正确作出辅助线构造直角三角形,用了方程思想.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为B′,折痕为EF.已知AB=AC=6,BC=8,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是
将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为B′,折痕为EF.已知AB=AC=6,BC=8,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是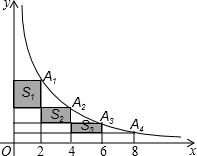 在反比例函数y=
在反比例函数y= 如图,AC是我校某教学大楼的高,在地面上B点处测得楼顶A的仰角为45°,沿BC方向前进8米到达D点,测得tan∠ADC=
如图,AC是我校某教学大楼的高,在地面上B点处测得楼顶A的仰角为45°,沿BC方向前进8米到达D点,测得tan∠ADC= 如图,在平行四边形ABCD中,点O为对角线AC的中点,EF过点O且垂直于AC,则四边形AFCE是菱形吗?请说出理由.
如图,在平行四边形ABCD中,点O为对角线AC的中点,EF过点O且垂直于AC,则四边形AFCE是菱形吗?请说出理由.