题目内容
4.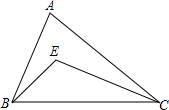 如图,△ABC中,∠ABC、∠ACB的平分线相交于点E.
如图,△ABC中,∠ABC、∠ACB的平分线相交于点E.(1)若∠ABC=60°,∠ACB=40°,求∠BEC;
(2)若∠ABC+∠ACB=100°,求∠BEC.
分析 (1)先根据∠ABC、∠ACB的平分线相交于点E,∠ABC=60°,∠ACB=40°求出∠EBC与∠ECB的度数,再由三角形内角和定理即可得出结论;
(2)根据∠ABC、∠ACB的平分线相交于点E,∠ABC+∠ACB=100°求出∠EBC+∠ECB的度数,再由三角形内角和定理即可得出结论.
解答 解:(1)∵∠ABC、∠ACB的平分线相交于点E,∠ABC=60°,∠ACB=40°,
∴∠EBC=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×60°=30°,∠ECB=$\frac{1}{2}$∠ACB=$\frac{1}{2}$×40°=20°,
∴∠BEC=180°-30°-20°=130°;
(2)∵∠ABC、∠ACB的平分线相交于点E,∠ABC+∠ACB=100°,
∴∠EBC+∠ECB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×100°=50°,
∴∠BEC=180°-50°=130°.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
19.下列不等式组是一元一次不等式组的是( )
| A. | $\left\{\begin{array}{l}{x-y>0}\\{x+y<0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+\frac{1}{3}>\frac{1}{2}x}\\{3x≠4x-1}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{{x}^{2}+x-2>0}\\{3x<0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{3x+2y=0}\\{x>-y}\end{array}\right.$ |
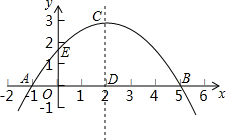 如图,抛物线y=ax2+bx+$\frac{5}{3}$经过点A(-1,0),对称轴方程x=2,请解答下列问题:
如图,抛物线y=ax2+bx+$\frac{5}{3}$经过点A(-1,0),对称轴方程x=2,请解答下列问题: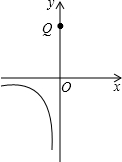 对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+$\frac{b}{k}$,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.例如:P(2,4)的“2属派生点”为P′(2+$\frac{4}{2}$,2×2+4),即P′(4,8).
对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+$\frac{b}{k}$,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.例如:P(2,4)的“2属派生点”为P′(2+$\frac{4}{2}$,2×2+4),即P′(4,8).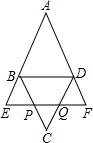 如图,四边形ABCD为平行四边形,EF∥BD,分别交BC,CD于点P,Q,交AB,AD的延长线于E,F,且BE=BP,求证:
如图,四边形ABCD为平行四边形,EF∥BD,分别交BC,CD于点P,Q,交AB,AD的延长线于E,F,且BE=BP,求证: