题目内容
13.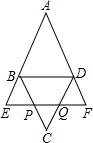 如图,四边形ABCD为平行四边形,EF∥BD,分别交BC,CD于点P,Q,交AB,AD的延长线于E,F,且BE=BP,求证:
如图,四边形ABCD为平行四边形,EF∥BD,分别交BC,CD于点P,Q,交AB,AD的延长线于E,F,且BE=BP,求证:(1)∠E=∠F;
(2)四边形ABCD是菱形.
分析 (1)首先判定四边形BPFD是平行四边形,所以BP∥DF,利用平行线的性质可得∠F=∠BPE,又因为BE=BP,可得∠E=∠F;
(2)利用平行线的性质以及菱形的判定方法进而得出即可.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴BP∥DF,
∵EF∥BD,
∴四边形BPFD是平行四边形,
∴BP∥DF,
∴∠F=∠BPE,
∵BE=BP,
∴∠E=∠BPE,
∴∠E=∠F;
(2)∵EF∥BD,
∴∠E=∠ABD,∠F=∠ADB
∴∠ABD=∠ADB,
又∵四边形ABCD为平行四边形,
∴四边形ABCD是菱形.
点评 本题考查了平行四边形的性质和判定、菱形的判定等知识,得出四边形BPFD是平行四边形是解题关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
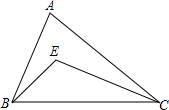 如图,△ABC中,∠ABC、∠ACB的平分线相交于点E.
如图,△ABC中,∠ABC、∠ACB的平分线相交于点E.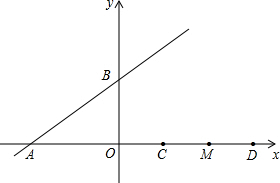 已知直线y=$\frac{3}{4}$x+b与x轴,y轴分别交于A,B两点,点D在x轴正半轴,且OD=6,点C,M是线段OD的三等分点(点C在点M的左侧)
已知直线y=$\frac{3}{4}$x+b与x轴,y轴分别交于A,B两点,点D在x轴正半轴,且OD=6,点C,M是线段OD的三等分点(点C在点M的左侧) 阅读下面一段材料,运用相关知识解决问题.
阅读下面一段材料,运用相关知识解决问题.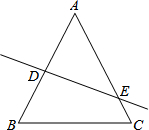 如图,己知AB=AC,DE垂直平分AB交AB于E点,若AB=12cm,BC=10cm,∠BAC=40°,求△BCE的周长和∠EBC的度数.
如图,己知AB=AC,DE垂直平分AB交AB于E点,若AB=12cm,BC=10cm,∠BAC=40°,求△BCE的周长和∠EBC的度数.