Question

19．在△ABC中，AB=AC，∠BAC=90°，点D在射线BC上（与B、C两点不重合），以AD为边作正方形ADEF，使点E与点B在直线AD的异侧，射线BA与射线CF相交于点G．
（1）若点D在线段BC上，如图1．
①依题意补全图1；
②判断BC与CG的数量关系与位置关系，并加以证明；
（2）若点D在线段BC的延长线上，且G为CF中点，连接GE，AB=$\sqrt{2}$，则GE的长为$\sqrt{10}$，并简述求GE长的思路．

Answer 1

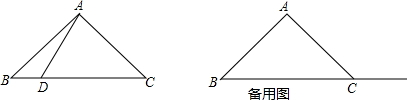
分析 （1）①依题意补全图形，如图1所示，②判断出△BAD≌△CAF即可；
（2）先判断出△BAD≌△CAF，得到BD=CF，BG⊥CF，得到直角三角形，利用勾股定理计算即可．

解答 （1）证明：①依题意补全图形，如图1所示，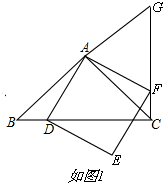

②BC⊥CG，BC=CG；
∵∠BAC=90°，AB=AC，
∴∠ABC=∠ACB=45°，
∵四边形ADEF是正方形，
∴AD=AF，∠DAF=90°，
∵∠BAC=∠BAD+∠DAC=90°，
∠DAF=∠CAF+∠DAC=90°，
∴∠BAD=∠CAF，
在△BAD和△CAF中，
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF}\end{array}\right.$
∴△BAD≌△CAF（SAS），
∴∠ACF=∠ABD=45°，
∴∠ACF+∠ACB=90°，
∴BC⊥CG；
∵点G是BA延长线上的点，
BC=CG
（2）如图2，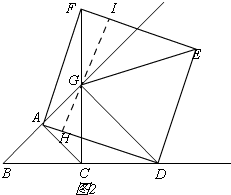

∵∠BAC=90°，AB=AC，
∴∠ABC=∠ACB=45°，
∵四边形ADEF是正方形，
∴AD=AF，∠DAF=90°，
∵∠BAC=∠BAD-∠DAC=90°，
∠DAF=∠CAF-∠DAC=90°，
∴∠BAD=∠CAF，
在△BAD和△CAF中，
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF}\end{array}\right.$
∴△BAD≌△CAF（SAS），
∴∠ACF=∠ABD=45°，BD=CF，
∴∠ACF+∠ACB=90°，
∴BC⊥CF；
∵AB=$\sqrt{2}$，BC=CD=CG=GF=2，
∴在Rt△AGH中，根据勾股定理得，AG=$\sqrt{2}$，
∴在Rt△AGH中，根据勾股定理的，DG=2$\sqrt{2}$，
∵AD=$\sqrt{10}$，
∴AH=$\frac{\sqrt{10}}{5}$，HG=$\frac{2\sqrt{10}}{5}$，
∴GI=AD-HG=$\frac{3\sqrt{10}}{5}$，
∴GE=$\sqrt{G{I}^{2}+I{E}^{2}}$=$\sqrt{10}$
故答案为$\sqrt{10}$．

点评 此题是四边形综合题，主要考查了全等三角形的性质和判定，垂直的判断方法，解本题的关键是判断出角相等．