题目内容
4.已知M=($\frac{3x}{x+1}$-$\frac{x}{x+1}$)×$\frac{{x}^{2}-1}{x}$+2,N=(1+$\frac{1}{x-1}$)÷$\frac{1}{{x}^{2}-1}$-(x-1),且x≠1.小丽和小军在对上述式子进行化简之后,小刚说不论x取何值(x≠1),M的值都比N的值大;小军说不论x取何值(x≠1),N的值都比M的值大.请你判断他们谁的结论正确,并说明理由.分析 先把M、N的式子进行化简,再作差比较其大小即可.
解答 解:小军的说法正确.
理由:∵M=$\frac{2x}{x+1}$•$\frac{(x+1)(x-1)}{x}$+2=2(x-1)+2=2x,
N=$\frac{x}{x-1}$•(x+1)(x-1)-x+1
=x(x+1)-x+1
=x2+1,
∴M-N=2x-x2-1=-(x2-2x+1)=-(x-1)2,
∵x≠1,
∴(x-1)2>0,
∴-(x-1)2<0,
∴M<N.
点评 本题考查的是分式的化简求值,熟知利用作差法比较分式的大小及分式混合运算的法则是解答此题的关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
14. 如图所示的几何体的三视图中,面积最大的为( )
如图所示的几何体的三视图中,面积最大的为( )
 如图所示的几何体的三视图中,面积最大的为( )
如图所示的几何体的三视图中,面积最大的为( )| A. | 主视图 | B. | 左视图 | C. | 俯视图 | D. | 一样大 |
15.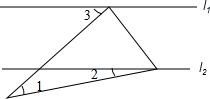 如图,一个直角三角尺的直角顶点和一个锐角顶点分别落在直线l1和l2上,且l1∥l2,∠1=30°,当∠2=10°时,∠3的度数是( )
如图,一个直角三角尺的直角顶点和一个锐角顶点分别落在直线l1和l2上,且l1∥l2,∠1=30°,当∠2=10°时,∠3的度数是( )
 如图,一个直角三角尺的直角顶点和一个锐角顶点分别落在直线l1和l2上,且l1∥l2,∠1=30°,当∠2=10°时,∠3的度数是( )
如图,一个直角三角尺的直角顶点和一个锐角顶点分别落在直线l1和l2上,且l1∥l2,∠1=30°,当∠2=10°时,∠3的度数是( )| A. | 45° | B. | 40° | C. | 35° | D. | 30° |
12.下列四个数中,最大的数是( )
| A. | |-3| | B. | 30 | C. | 3-1 | D. | $\sqrt{3}$ |
9. 一个三棱柱如图所示,它的主视图是( )
一个三棱柱如图所示,它的主视图是( )
 一个三棱柱如图所示,它的主视图是( )
一个三棱柱如图所示,它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
14.下列方程中,是二元一次方程的是( )
| A. | xy-1=0 | B. | x2+y=3 | C. | $\frac{x}{4}$=3y-1 | D. | x-$\frac{1}{y}$=2 |
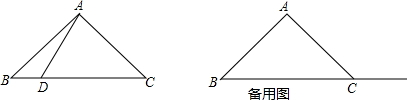
 如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当r=$\sqrt{2}$时,S为$\frac{π}{2}$-1.
如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当r=$\sqrt{2}$时,S为$\frac{π}{2}$-1.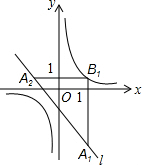 如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=$\frac{1}{x}$,在l上取一点A1,过A1作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2=-$\frac{3}{2}$,a2016=-$\frac{1}{3}$;若要将上述操作无限次地进行下去,则a1不可能取的值是0或-1.
如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=$\frac{1}{x}$,在l上取一点A1,过A1作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2=-$\frac{3}{2}$,a2016=-$\frac{1}{3}$;若要将上述操作无限次地进行下去,则a1不可能取的值是0或-1.