Question

10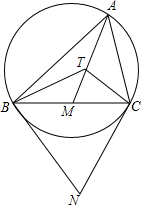．已知锐角△ABC及其外接圆，AM是边BC的中线，分别过点B，C作外接圆的切线，两条切线交于点N，T是AM上的一点，且∠ATC=∠ABN，求证：$\frac{AB}{AC}=\frac{TB}{TC}$．

Answer 1

分析 如图，延长CT交△ABC外接圆于H，连接AH、BH，延长AM交△ABC外接圆于K，连接BK、CK，先证明△ABH∽△ACT，得$\frac{AB}{AC}$=$\frac{BH}{TC}$，再证明BH=BT即可．

解答 证明：如图，延长CT交△ABC外接圆于H，连接AH、BH，延长AM交△ABC外接圆于K，连接BK、CK．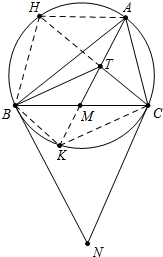
∵NB是⊙O切线，
∴∠ABN=∠AHB，
∵∠ATC=∠ABN，
∴∠AHE=∠ATC，
∵∠ACT=∠ABH，
∴△ABH∽△ACT，
∴$\frac{AB}{AC}$=$\frac{BH}{TC}$，∠HAB=∠KAC，
∴$\widehat{BH}$=$\widehat{KC}$，
∴∠BCH=∠CBK，
∴BK∥HC，
在△TCM和△KBM中，
$\left\{\begin{array}{l}{∠TMC=∠BMK}\\{∠TCB=∠MBK}\\{CM=BM}\end{array}\right.$，
∴△TCM≌△KBM，
∴TM=BK，
∵BM=MC，
∴四边形BKCT是平行四边形，
∴∠BTH=∠KCT，
∵$\widehat{HK}$=$\widehat{BC}$，
∴∠BHT=∠KCH，
∴∠BHT=∠BTH，
∴BH=BT，
∴$\frac{AB}{AC}$=$\frac{BT}{TC}$．

点评 本题考查相似三角形的判定和性质、切线的性质、圆、平行四边形的判定和性质、等腰三角形的判定等知识，解题的关键是添加辅助线构造相似三角形，题目比较难，属于中考压轴题．