题目内容
4.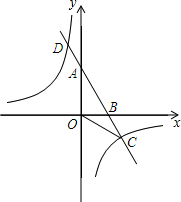 如图,已知A,B两点的坐标分别是A(0,2$\sqrt{3}$),B(2,0),直线AB与反比例函数y=$\frac{m}{x}$的图象交于点C和点D(-1,a).
如图,已知A,B两点的坐标分别是A(0,2$\sqrt{3}$),B(2,0),直线AB与反比例函数y=$\frac{m}{x}$的图象交于点C和点D(-1,a).(1)求直线AB和反比例函数的解析式;
(2)连接OD,求△COD的面积.
分析 (1)根据A,B两点的坐标分别是A(0,2$\sqrt{3}$),B(2,0),可以求得直线AB的解析式,根据直线AB与反比例函数y=$\frac{m}{x}$的图象交于点C和点D(-1,a),可以求得点D的坐标,从而可以求得反比例函数的解析式;
(2)根据直线AB与反比例函数y=$\frac{m}{x}$的图象交于点C和点D(-1,a),可以求得点C的坐标,由图可知△COD的面积等于△DOB与△OBC的面积之和,本题得以解决.
解答 解:(1)设过点A、B的直线的解析式为y=kx+b,
∵A,B两点的坐标分别是A(0,2$\sqrt{3}$),B(2,0),
∴$\left\{\begin{array}{l}{b=2\sqrt{3}}\\{2k+b=0}\end{array}\right.$
解得,$\left\{\begin{array}{l}{k=-\sqrt{3}}\\{b=2\sqrt{3}}\end{array}\right.$
即直线AB的解析式为y=$-\sqrt{3}x+2\sqrt{3}$,
将x=-1代入y=$-\sqrt{3}x+2\sqrt{3}$,得y=3$\sqrt{3}$,
∴点D的坐标为(-1,3$\sqrt{3}$),
∵点D在反比例函数y=$\frac{m}{x}$的图象上,
∴$3\sqrt{3}=\frac{m}{-1}$,
解得,m=-3$\sqrt{3}$,
即反比例函数的解析式是$y=\frac{-3\sqrt{3}}{x}$;
(2)连接OD,如右图所示,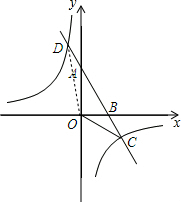
$\left\{\begin{array}{l}{y=\frac{-3\sqrt{3}}{x}}\\{y=-\sqrt{3}x+2\sqrt{3}}\end{array}\right.$
解得,$\left\{\begin{array}{l}{x=-1}\\{y=3\sqrt{3}}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=-\sqrt{3}}\end{array}\right.$
∴点C的坐标是(3,$-\sqrt{3}$),
∵点D的坐标是(-1,3$\sqrt{3}$),点B的坐标是(2,0),
∴S△COD=S△DOB+S△OBC=$\frac{2×3\sqrt{3}}{2}+\frac{2×\sqrt{3}}{2}=4\sqrt{3}$,
即△COD的面积是4$\sqrt{3}$.
点评 本题考查反比例函数与一次函数的交点问题,解题的关键是明确题意,找出所求问题需要的条件.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | -a2-b2 | B. | a2+b2 | C. | -4a2+12ab-9 | D. | 25m2+15n+9 |
部分时段车流量情况调查表
| 时间 | 负责组别 | 车流总量 | 每分钟车流量 |
| 早晨上学6:30~7:00 | ①② | 2747 | 92 |
| 中午放学11:20~11:50 | ③④ | 1449 | 48 |
| 下午放学5:00~5:30 | ⑤⑥ | 3669 | 122 |
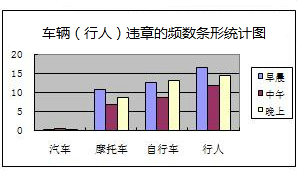 回答下列问题:
回答下列问题:(1)请你写出2条交通法规:①红灯停、绿灯行,②过马路要走人行横道线;
(2)早晨、中午、晚上三个时段每分钟车流量的极差是74,这三个时段的车流总量的中位数是2747;
(3)观察表中的数据及条形统计图,写出你发现的一个现象并分析其产生的原因;
(4)通过分析写一条合理化建议.
| A. | $\frac{1}{a{b}^{2}}$$\sqrt{ab}$ | B. | $\frac{1}{{a}^{2}b}$$\sqrt{ab}$ | C. | $\frac{1}{b}\sqrt{ab}$ | D. | b$\sqrt{ab}$ |
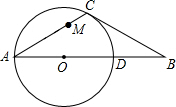 如图,在△ABC中,CA=CB,∠CAB=30°,⊙O经过点C,且圆的直径AD在线段AB上.
如图,在△ABC中,CA=CB,∠CAB=30°,⊙O经过点C,且圆的直径AD在线段AB上.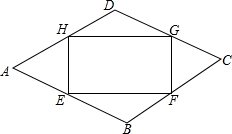 如图,点E、F、G、H分别在菱形ABCD的四条边上,BE=BF=DG=DH,连接EF,FG,GH,HE,已知∠A=60°.
如图,点E、F、G、H分别在菱形ABCD的四条边上,BE=BF=DG=DH,连接EF,FG,GH,HE,已知∠A=60°.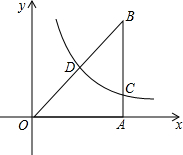 已知,Rt△OAB在直角坐标系内的位置如图所示,BA⊥OA,点B(4,4),反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过线段OB的中点D,且与直线AB交于点C.
已知,Rt△OAB在直角坐标系内的位置如图所示,BA⊥OA,点B(4,4),反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过线段OB的中点D,且与直线AB交于点C.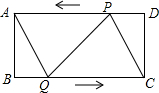 如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P、Q的速度的速度都是1cm/s,连结PQ,AQ,CP,设点P、Q运动的时间为t(s).
如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P、Q的速度的速度都是1cm/s,连结PQ,AQ,CP,设点P、Q运动的时间为t(s).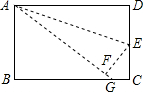 如图,点E是矩形ABCD的边CD的中点,将△ADE沿AE折叠后得到△AEF,点F在矩形ABCD内部,延长AF交BC于G.
如图,点E是矩形ABCD的边CD的中点,将△ADE沿AE折叠后得到△AEF,点F在矩形ABCD内部,延长AF交BC于G.