Question

3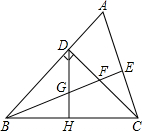．如图，在△ABC中，∠ABC=45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，BE与CD相交于点F，BF=2CE，H是BC边的中点，连接DH与BE相交于点G．下列结论中：①∠A=67.5°；②DF=AD；③BE=2BG；④DH⊥BC，正确的个数是（　　）

• A． 1个
• B． 2个
• C． 3个
• D． 4个

Answer 1

分析 根据已知条件得到△BCD是等腰直角三角形，由等腰直角三角形的性质得到BD=CD，由BE平分∠ABC，得到∠ABE=22.5°，根据三角形的内角和得到∠A=67.5°；故①正确；根据余角得到性质得到∠DBF=∠ACD，根据全等三角形的性质得到AD=DF，故②正确；根据BE平分∠ABC，且BE⊥AC于E，得到∠ABE=∠CBE，∠AEB=∠CEB=90°，根据全等三角形的性质得到AE=CE=$\frac{1}{2}$AC，求得BE⊥AC，由于△BCD是等腰直角三角形，H是BC边的中点，得到DH⊥BC，故④正确；推出DH不平行于AC，于是得到BE≠2BG，故③错误．

解答 解：∵∠ABC=45°，CD⊥AB于D，
∴△BCD是等腰直角三角形，
∴BD=CD，
∵BE平分∠ABC，
∴∠ABE=22.5°，
∴∠A=67.5°；故①正确；
∵CD⊥AB于D，BE⊥AC于E，
∴∠DBF+∠A=90°，∠ACD+∠A=90°，
∴∠DBF=∠ACD，
在△BDF与△CDA中，
$\left\{\begin{array}{l}{∠DBF=∠ACD}\\{BD=CD}\\{∠BDF=∠CDA=90°}\end{array}\right.$，
∴△BDF≌△CDA（ASA），
∴AD=DF，故②正确；
∵BE平分∠ABC，且BE⊥AC于E，
∴∠ABE=∠CBE，∠AEB=∠CEB=90°，
∴在△ABE与△CBE中，
$\left\{\begin{array}{l}{∠ABE=∠CBE}\\{BE=BE}\\{∠AEB=CEB=90°}\end{array}\right.$，
∴△ABE≌△CBE（ASA），
∴AE=CE=$\frac{1}{2}$AC，
∴BE⊥AC，
∵△BCD是等腰直角三角形，H是BC边的中点，
∴DH⊥BC，故④正确；
∴DH不平行于AC，
∵BH=CH，∴BG≠EG；
∴BE≠2BG，故③错误．
故选C．

点评 本题考查了等腰直角三角形的判定与性质，角平分线的性质，全等三角形的判定与性质，仔细分析图形并熟练掌握各性质是解题的关键．