题目内容
3. 如图,平行四边形ABCD中,点E为AD的中点,连CE,点M、N为CE上两点,且BM∥DN.
如图,平行四边形ABCD中,点E为AD的中点,连CE,点M、N为CE上两点,且BM∥DN.(1)求证:BM=2DN;
(2)连DM并延长交AB于F,若BF=2AF,求$\frac{DM}{MF}$的值.
分析 (1)欲证明BM=2DN,只需求得相似三角形△EDN∽△CBM的相似比即可;
(2)取BF、BM的中点H、Q,连接HQ、AQ,则HQ是三角形的中位线,所以MF=2QH,根据BF=2AF,得出AF=HF,得出PF是△AQH的中位线,得出QH=2PF,MF=2QH=4PF,PM=3PF,同理:求得DM=PM=3PF,即可求得$\frac{DM}{MF}$的值.
解答 (1)证明:∵点E为AD的中点,
∴DE=$\frac{1}{2}$AD,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠DEN=∠BCM,ED=$\frac{1}{2}$CB
又∵BM∥DN,
∴∠END=∠CMB,
∴△EDN∽△CBM,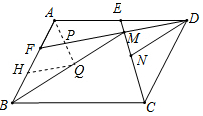
∴$\frac{DN}{BM}=\frac{ED}{CB}$=$\frac{1}{2}$,
∴BM=2DN;
﹙2﹚解:如图2,取BF、BM的中点,H、Q,连接HQ、AQ,
∵BQ=MQ,BH=HF,
∴QH∥DF,
∴MF=2QH,
∵BF=2AF,
∴AF=HF,
∴PF是△AQH的中位线,
∴QH=2PF,
∴MF=2QH=4PF,
∴PM=3PF,
同理:EM是△ADP的中位线,
∴DM=PM=3PF,
∴$\frac{DM}{MF}=\frac{3PF}{4PF}$=$\frac{3}{4}$.
点评 本题考查了平行四边形的性质,三角形的中位线定理,三角形相似的判定和性质,熟练掌握平行四边形的性质,证明三角形相似是解决问题的关键.

练习册系列答案
相关题目
 如图,直线AB经过点O,根据图形解答下列问题:
如图,直线AB经过点O,根据图形解答下列问题: 求出图中所示的正三棱柱展开图的面积(结果保留根号)
求出图中所示的正三棱柱展开图的面积(结果保留根号) 如图,某水库大坝的横断面是梯形ABCD,坝顶宽CD=3m,坡角A为30°,坝高DE=8m,坝底宽AB为(27+8$\sqrt{3}$)m,试求迎水坡BC的长和迎水坡BC的坡度.
如图,某水库大坝的横断面是梯形ABCD,坝顶宽CD=3m,坡角A为30°,坝高DE=8m,坝底宽AB为(27+8$\sqrt{3}$)m,试求迎水坡BC的长和迎水坡BC的坡度.
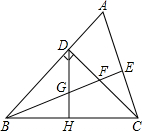 如图,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,BE与CD相交于点F,BF=2CE,H是BC边的中点,连接DH与BE相交于点G.下列结论中:①∠A=67.5°;②DF=AD;③BE=2BG;④DH⊥BC,正确的个数是( )
如图,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,BE与CD相交于点F,BF=2CE,H是BC边的中点,连接DH与BE相交于点G.下列结论中:①∠A=67.5°;②DF=AD;③BE=2BG;④DH⊥BC,正确的个数是( )