题目内容
11. 如图,△ABC内接于⊙O,AD⊥BC于D,BE⊥AC于E,AD交⊙O于F,交BE于H,连DE,试探究DE与直径CG有无特殊的位置关系?
如图,△ABC内接于⊙O,AD⊥BC于D,BE⊥AC于E,AD交⊙O于F,交BE于H,连DE,试探究DE与直径CG有无特殊的位置关系?
分析 结论:DE⊥CG.由△CAD∽△CBE,推出$\frac{CA}{CB}$=$\frac{CD}{CE}$,推出$\frac{CA}{CD}$=$\frac{CB}{CE}$,由∠ECD=∠BCA,推出△ECD∽△BCA,推出∠CED=∠ABC=∠G,由CG是直径,推出∠GAC=90°,推出∠G+∠ACG=90°,推出∠ACG+∠DEC=90°,即可证明∠EKC=90°.
解答 解:结论:DE⊥CG.
理由:如图,连接AG,DE交CG于K.
∵AD⊥BC,BE⊥AC,
∴∠AEB=∠BEC=∠ADB=∠ADC=90°,
∵∠AHE=∠BHD,
∴∠CAD=∠CBE,
∴△CAD∽△CBE,
∴$\frac{CA}{CB}$=$\frac{CD}{CE}$,
∴$\frac{CA}{CD}$=$\frac{CB}{CE}$,∵∠ECD=∠BCA,
∴△ECD∽△BCA,
∴∠CED=∠ABC=∠G,
∵CG是直径,
∴∠GAC=90°,
∴∠G+∠ACG=90°,
∴∠ACG+∠DEC=90°,
∴∠EKC=90°,
∴DE⊥CG.
点评 本题考查三角形的外接圆与外心、相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形,利用相似三角形的性质解决问题,属于中考常考题型.

练习册系列答案
相关题目
6. 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=8,则CP的长为( )
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=8,则CP的长为( )
 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=8,则CP的长为( )
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=8,则CP的长为( )| A. | 3 | B. | 3.5 | C. | 4 | D. | 4.5 |
16.在Rt△ABC中,∠C=90°,AB=4,AC=2$\sqrt{2}$,则∠A的度数为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
 求出图中所示的正三棱柱展开图的面积(结果保留根号)
求出图中所示的正三棱柱展开图的面积(结果保留根号)
 如图,AB是⊙O的直径,且AB=10,弦MN的长为8,若弦MN的两端在圆周上滑动,始终与AB相交.记点A,B到MN的距离为h1,h2.则|h1-h2|等于( )
如图,AB是⊙O的直径,且AB=10,弦MN的长为8,若弦MN的两端在圆周上滑动,始终与AB相交.记点A,B到MN的距离为h1,h2.则|h1-h2|等于( )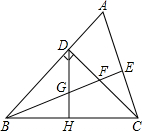 如图,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,BE与CD相交于点F,BF=2CE,H是BC边的中点,连接DH与BE相交于点G.下列结论中:①∠A=67.5°;②DF=AD;③BE=2BG;④DH⊥BC,正确的个数是( )
如图,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,BE与CD相交于点F,BF=2CE,H是BC边的中点,连接DH与BE相交于点G.下列结论中:①∠A=67.5°;②DF=AD;③BE=2BG;④DH⊥BC,正确的个数是( ) 已知:如图,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G,请写出GE:CE的比值,并加以证明.
已知:如图,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G,请写出GE:CE的比值,并加以证明.