题目内容
14.抛物线y=ax2+bx+c的符号问题:(1)a的符号由抛物线的开口方向确定;
(2)b的符号由抛物线的对称轴的位置确定;
(3)c的符号由抛物线与y轴交点所在位置确定;
(4)b2-4ac的符号由抛物线的与x轴交点的个数确定;
(5)a+b+c的符号由x=1在抛物线上的点的位置确定;
(6)a-b+c的符号由x=-1在抛物线的点的位置确定;
(7)2a+b的符号由抛物线对称轴与x轴交点的位置确定;
(8)2a-b的符号由抛物线开口方向与对称轴的位置确定.
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:(1)a的符号由抛物线的 开口方向确定;
(2)b的符号由抛物线的 对称轴的位置确定;
(3)c的符号由抛物线 与y轴交点所在位置确定;
(4)b2-4ac的符号由抛物线的 与x轴交点的个数确定;
(5)a+b+c的符号由 x=1在抛物线上的点的位置确定;
(6)a-b+c的符号由 x=-1在抛物线的点的位置确定;
(7)2a+b的符号由抛物线 对称轴与 x轴交点的位置确定;
(8)2a-b的符号由抛物线 开口方向与 对称轴的位置确定.
故答案是:(1)开口方向;(2)对称轴的位置;(3)与y轴交点所在位置;(4)与x轴交点的个数;(5)x=1;(6)x=-1;(7)对称轴;x轴的交点;(8)开口方向;对称轴.
点评 主要考查图象与二次函数系数之间的关系,二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.将抛物线y=3x2先向左平移1个单位,再向下平移4个单位,所得到的新抛物线是( )
| A. | y=3(x+1)2-4 | B. | y=3(x-1)2-4 | C. | y=3(x+1)2+4 | D. | y=3(x-1)2+4 |
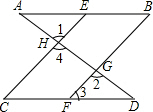 补全下列推理过程及括号内的推理依据:
补全下列推理过程及括号内的推理依据: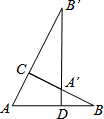 如图,Rt△ABC中,∠ACB=90°,AC=1,BC=2.将△ABC绕顶点C旋转,点A转到BC边上的点A′处,点B转到点B′处.延长B′A′交AB于点D,则S△BA′D=$\frac{1}{5}$.
如图,Rt△ABC中,∠ACB=90°,AC=1,BC=2.将△ABC绕顶点C旋转,点A转到BC边上的点A′处,点B转到点B′处.延长B′A′交AB于点D,则S△BA′D=$\frac{1}{5}$. 抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),B(3,0)两点,与y轴交于点C(0,-3).
抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),B(3,0)两点,与y轴交于点C(0,-3).