题目内容
6. 抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),B(3,0)两点,与y轴交于点C(0,-3).
抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),B(3,0)两点,与y轴交于点C(0,-3).(1)求该抛物线的解析式及顶点M的坐标;
(2)当y的值大于0时,求x的取值范围;
(3)分别求出△BCM与△ABC的面积.
分析 (1)由于已知抛物线与x轴的交点坐标,则可设交点式y=a(x+1)(x-3),然后把(0,-3)代入求出a即可得到抛物线解析式,再配成顶点式得到M点坐标;
(2)观察函数图象,写出抛物线在x轴上方部分所对应的自变量的范围即可;
(3)根据三角形面积公式计算△ABC的面积,利用S△BCM=S梯形OCMD+S△BMD-S△BOC计算△BCM的面积.
解答 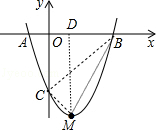 解:(1)设抛物线解析式为y=a(x+1)(x-3),
解:(1)设抛物线解析式为y=a(x+1)(x-3),
∵抛物线过点(0,-3),
∴-3=a(0+1)(0-3),
∴a=1,
∴抛物线解析式为y=(x+1)(x-3),即y=x2-2x-3,
∵y=x2-2x-3=(x-1)2-4,
∴顶点M(1,-4);
(2)x<-1或x>3;
(3)如图,连接BC、BM、CM,作MD⊥x轴于D,
S△BCM=S梯形OCMD+S△BMD-S△BOC=$\frac{1}{2}$×(3+4)×1+$\frac{1}{2}$×2×4-$\frac{1}{2}$×3×3=3
S△ABC=$\frac{1}{2}$×4×3=6.
点评 本题考查了抛物线与x轴的交点:从二次函数的交点式y=a(x-x1)(x-x2)(a,b,c是常数,a≠0)可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0).也考查了待定系数法求抛物线解析式和三角形面积公式.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
1.某射手在相同条件下进行射击训练,结果如下表所示:
(1)计算并填写表中击中靶心的频率;
(2)试根据该表,估计这名射手射击一次,击中靶心的概率约为多少?并说明理由.
| 射击次数n | 10 | 20 | 50 | 100 | 200 | 500 |
| 击中靶心次数m | 9 | 19 | 44 | 91 | 178 | 450 |
| 击中靶心频率$\frac{m}{n}$ |
(2)试根据该表,估计这名射手射击一次,击中靶心的概率约为多少?并说明理由.
15.计算a6(a2)3的结果等于( )
| A. | a11 | B. | a12 | C. | a14 | D. | a36 |
16.某自行车计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天产量与计划量相比有出入.下表是某周的生产情况(超产记为正、减产记为负):
(1)根据记录的数据可知该厂星期四生产自行车213辆;
(2)根据记录的数据可知该厂本周实际生产自行车1409辆;
(3)该厂实行每周计件工资制,每生产一辆可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣20元,那么该厂工人这一周的工资总额是多少?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
(2)根据记录的数据可知该厂本周实际生产自行车1409辆;
(3)该厂实行每周计件工资制,每生产一辆可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣20元,那么该厂工人这一周的工资总额是多少?
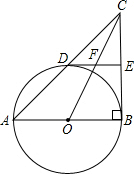 如图,Rt△ABC中,∠ABC=90°,以AB为直径作圆O交AC边于点D,E是边BC的中点,连结OC交DE于点F.
如图,Rt△ABC中,∠ABC=90°,以AB为直径作圆O交AC边于点D,E是边BC的中点,连结OC交DE于点F.