题目内容
2. 如图所示,在?ABCD中,M,N是对角线BD上的两点,BN=DM,请判断AM与CN有怎样的数量关系,并说明理由,它们的位置关系如何呢?
如图所示,在?ABCD中,M,N是对角线BD上的两点,BN=DM,请判断AM与CN有怎样的数量关系,并说明理由,它们的位置关系如何呢?
分析 根据平行四边形的性质得到AD=BC,AD∥BC,由平行线的性质得到∠ADM=∠CBN,推出△ADM≌△CBN,根据全等三角形的性质得到AM=CN,∠AMN=∠BNC,由平行线的判定即可得到结论.
解答 解:AM=CN,AM∥CN,
在?ABCD中,
∵AD=BC,AD∥BC,
∴∠ADM=∠CBN,
在△ADM与△CBN中,$\left\{\begin{array}{l}{AD=BC}\\{∠ADM=∠CBN}\\{DM=BN}\end{array}\right.$,
∴△ADM≌△CBN,
∴AM=CN,∠AMN=∠BNC,
∴AM∥CN.
点评 此题考查了平行四边形的性质与全等三角形的判定与性质.此题比较简单,注意掌握平行四边形的对边平行且相等,注意数形结合思想的应用.

练习册系列答案
相关题目
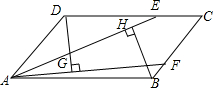 如图,在平行四边形ABCD中,点E,F分别在BC,CD上,且AE=AF,DG⊥AE,BH⊥AF,点G,H为垂足,猜想DG与BH的大小关系,并证明你的猜想.
如图,在平行四边形ABCD中,点E,F分别在BC,CD上,且AE=AF,DG⊥AE,BH⊥AF,点G,H为垂足,猜想DG与BH的大小关系,并证明你的猜想.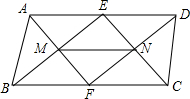 如图所示,已知在?ABCD中,E,F分别是AD,BC的中点,求证:MN∥BC.
如图所示,已知在?ABCD中,E,F分别是AD,BC的中点,求证:MN∥BC.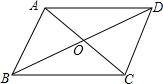 平行四边形ABCD的两条对角线AC,BD相交于点O.
平行四边形ABCD的两条对角线AC,BD相交于点O. 八年级(3)班同学要在广场上布置一个矩形的花坛,计划用红花摆成两条对角线,如果一条对角线用了38盆红花,还需要从花房运来多少盆红花?为什么?如果一条对角线用了49盆呢?
八年级(3)班同学要在广场上布置一个矩形的花坛,计划用红花摆成两条对角线,如果一条对角线用了38盆红花,还需要从花房运来多少盆红花?为什么?如果一条对角线用了49盆呢?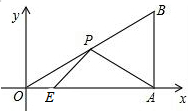 在平面直角坐标系中,Rt△OAB的顶点A在x轴上,点A的坐标为(3,0),∠AOB=30°,点E的坐标为($\frac{1}{2}$,0),点P为斜边OB上的一个动点,则PA+PE的最小值为$\frac{\sqrt{31}}{2}$.
在平面直角坐标系中,Rt△OAB的顶点A在x轴上,点A的坐标为(3,0),∠AOB=30°,点E的坐标为($\frac{1}{2}$,0),点P为斜边OB上的一个动点,则PA+PE的最小值为$\frac{\sqrt{31}}{2}$.