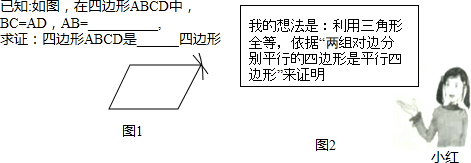
题目内容
12.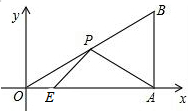 在平面直角坐标系中,Rt△OAB的顶点A在x轴上,点A的坐标为(3,0),∠AOB=30°,点E的坐标为($\frac{1}{2}$,0),点P为斜边OB上的一个动点,则PA+PE的最小值为$\frac{\sqrt{31}}{2}$.
在平面直角坐标系中,Rt△OAB的顶点A在x轴上,点A的坐标为(3,0),∠AOB=30°,点E的坐标为($\frac{1}{2}$,0),点P为斜边OB上的一个动点,则PA+PE的最小值为$\frac{\sqrt{31}}{2}$.
分析 过点E作E关于OB的对称点C,连接AC与OB相交,根据轴对称确定最短路线问题AC与OB的交点即为所求的点P,PA+PE的最小值为AC,过点C作CD⊥OA于D,求出CE,∠OEC=60°,再求出ED、CD,然后求出AD,再利用勾股定理列式计算即可得解.
解答 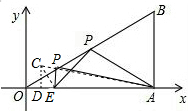 解:如图,过点E作E关于OB的对称点C,连接AC与OB相交,
解:如图,过点E作E关于OB的对称点C,连接AC与OB相交,
则AC与OB的交点即为所求的点P,PA+PE的最小值=AC,
过点C作CD⊥OA于D,
∵点C的坐标为($\frac{1}{2}$,0),且∠AOB=30°,
∴OC=$\frac{1}{2}$,CE=1×1×$\frac{1}{2}$=$\frac{1}{2}$,
∠OEC=90°-30°=60°,
∴ED=$\frac{1}{2}$×$\frac{1}{2}$=$\frac{1}{4}$,CD=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$,
∵顶点A的坐标为(3,0),点E的坐标为($\frac{1}{2}$,0),∠OAB=90°,
∴AE=3-$\frac{1}{2}$=$\frac{5}{2}$,
∴AD=$\frac{5}{2}$+$\frac{1}{4}$=$\frac{11}{4}$,
在Rt△ACD中,由勾股定理得,AC=$\sqrt{(\frac{11}{4})^{2}+(\frac{\sqrt{3}}{4})^{2}}$=$\frac{\sqrt{31}}{2}$.
故答案为:$\frac{\sqrt{31}}{2}$.
点评 本题考查了轴对称确定最短路线问题,坐标与图形性质,解直角三角形,熟练掌握最短路径的确定方法找出点P的位置以及表示PA+PE的最小值的线段是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | y1<y3<y2 | B. | y1<y2<y3 | C. | y3<y2<y1 | D. | y3<y1<y2 |
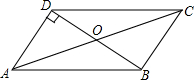 如图,在?ABCD中,∠ODA=90°,AC=20cm,BD=12cm,则AD的长为( )
如图,在?ABCD中,∠ODA=90°,AC=20cm,BD=12cm,则AD的长为( )| A. | 8cm | B. | 10cm | C. | 12cm | D. | 16cm |
 如图所示,在?ABCD中,M,N是对角线BD上的两点,BN=DM,请判断AM与CN有怎样的数量关系,并说明理由,它们的位置关系如何呢?
如图所示,在?ABCD中,M,N是对角线BD上的两点,BN=DM,请判断AM与CN有怎样的数量关系,并说明理由,它们的位置关系如何呢?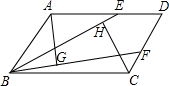 已知:如图,在平行四边形ABCD中,E、F分别为边AD、CD上一点,且BE=BF,AG⊥BF于F,CH⊥BE于H,求证:AG=CH.
已知:如图,在平行四边形ABCD中,E、F分别为边AD、CD上一点,且BE=BF,AG⊥BF于F,CH⊥BE于H,求证:AG=CH.