题目内容
20.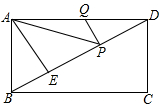 如图,BD为矩形ABCD的对角线,AE⊥BD,垂足为E,tan∠BAE=$\frac{\sqrt{3}}{3}$,BE=1,点P、Q分别在BD、AD上,连接AP、PQ,则AP+PQ的最小值为3.
如图,BD为矩形ABCD的对角线,AE⊥BD,垂足为E,tan∠BAE=$\frac{\sqrt{3}}{3}$,BE=1,点P、Q分别在BD、AD上,连接AP、PQ,则AP+PQ的最小值为3.
分析 设A点关于BD的对称点A′,连接A′D,可证明△ADA′为等边三角形,当PQ⊥AD时,则PQ最小,所以当A′Q⊥AD时AP+PQ最小,从而可求得AP+PQ的最小值等于DE的长,可得出答案.
解答 解: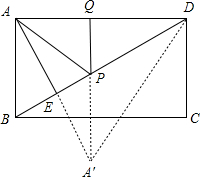
∵四边形ABCD为矩形,且AE⊥BD,tan∠BAE=$\frac{\sqrt{3}}{3}$,BE=1,
∴AB=2,AE=$\sqrt{3}$,
∵tan∠BAE=$\frac{\sqrt{3}}{3}$,
∴∠BAE=30°,
∴∠EAD=60°,
∵AE=$\sqrt{3}$,
∴DE=3,
如图,设A点关于BD的对称点为A′,连接A′D,PA′,
则A′A=2AE=2$\sqrt{3}$,AD=A′D=2$\sqrt{3}$,
∴△AA′D是等边三角形,
∵PA=PA′,
∴当A′、P、Q三点在一条线上时,A′P+PQ最小,
又垂线段最短可知当PQ⊥AD时,A′P+PQ最小,
∴AP+PQ=A′P+PQ=A′Q=DE=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题主要考查轴对称的应用,利用最小值的常规解法确定出A的对称点,从而确定出AP+PQ的最小值的位置是解题的关键,利用条件证明△A′DA是等边三角形,借助几何图形的性质可以减少复杂的计算.

练习册系列答案
相关题目
10.为加快建设经济强、环境美、后劲足、群众富的实力微山,魅力微山,活力微山,幸福微山;聚力脱贫攻坚,全面完成脱贫任务,某乡镇特制定一系列帮扶甲、乙两贫困村的计划,现决定从某地运送1225箱鱼苗到甲、乙两村养殖.若用大、小货车共20辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力和其运往甲、乙两村的运费如表:
(1)求这20辆车中大、小货车各多少辆?
(2)现安排其中16辆货车前往甲村,其余货车前往乙村,设前往甲村的大货车为x辆,前往甲、乙两村总费用为y元,试求出y与x的函数解析式及x的取值范围;
(3)在(2)的条件下,若运往甲村的鱼苗不少于980箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
| 车型 | 载货能力(箱/辆) | 运费 | |
| 甲村(元/辆) | 乙村(元/辆) | ||
| 大货车 | 70 | 800 | 900 |
| 小货车 | 35 | 400 | 600 |
(2)现安排其中16辆货车前往甲村,其余货车前往乙村,设前往甲村的大货车为x辆,前往甲、乙两村总费用为y元,试求出y与x的函数解析式及x的取值范围;
(3)在(2)的条件下,若运往甲村的鱼苗不少于980箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
5. 如图,半径为2的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是( )
如图,半径为2的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是( )
 如图,半径为2的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是( )
如图,半径为2的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是( )| A. | 18$\sqrt{3}$-6π | B. | 4$\sqrt{3}$-$\frac{4}{3}$π | C. | 9$\sqrt{3}$-$\frac{9}{2}$π | D. | 2$\sqrt{3}$-$\frac{2}{3}$π |
12. 亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名涌中学生,根据调查结果得到如图所示的统计图表.
亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名涌中学生,根据调查结果得到如图所示的统计图表.
请根据图表信息解答下列问题:
(1)a=35;
(2)补全条形统计图;
(3)据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.
 亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名涌中学生,根据调查结果得到如图所示的统计图表.
亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名涌中学生,根据调查结果得到如图所示的统计图表.| 类别 | 时间t(小时) | 人数 |
| A | t≤0.5 | 5 |
| B | 0.5<t≤1 | 20 |
| C | 1<t≤1.5 | a |
| D | 1.5<t≤2 | 30 |
| E | t>2 | 10 |
(1)a=35;
(2)补全条形统计图;
(3)据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.
 如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上),网格中小正方形的边长为1.
如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上),网格中小正方形的边长为1.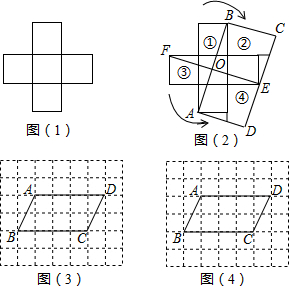
 抛物线F与x轴相交于A、B两点(点A在点B的左边),对称轴为直线x=1,顶点C在直线y=x-5上,与y轴相交于点D(0,3).
抛物线F与x轴相交于A、B两点(点A在点B的左边),对称轴为直线x=1,顶点C在直线y=x-5上,与y轴相交于点D(0,3).