题目内容
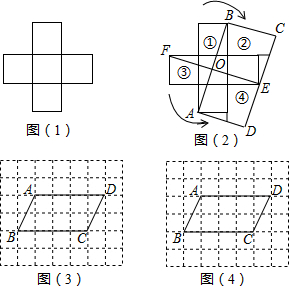
15.阅读下列材料,完成相应学习任务.问题:如图是一个由5个相同的正方形组成的十字形的纸片,把这一纸片沿一条直线截成两部分,然后把其中的一部分再沿着另一条直线截成两部分,使所得的三部分纸片通过适当的拼接能组成两个并列的全等的正方形,请在图中画出分割线及拼接后的图形.
分析:若设拼成的正方形的边长为x,十字形纸片中每个小正方形的边长为1,则2x2=5.解得x=$\frac{\sqrt{10}}{2}$,所以拼成的两个小正方形的边长为$\frac{\sqrt{10}}{2}$.如图(2)连接AB,根据勾股定理得AB=$\sqrt{10}$,所以AB的长度为所要拼成的两个小正方形边长的2倍,于是可得图(2)所示的拼法.
请你参考材料中思考问题的方法,解决下列问题:
图(3)、图(4)是由边长为1的小正方形组成的网格图,平行四边形ABCD的四个顶点均在格点上,请将图中的平行四边形ABCD进行适当的剪拼,使得分割后的各部分能拼成符合要求的新图形.
要求:
(1)在图(3)、图(4)中画出分割线及拼接后的图形,所拼接的各部分之间不能互相重叠,不能留有空隙;
(2)图(3)中拼出的图形是等腰三角形,图(4)中拼出的图形是正方形.
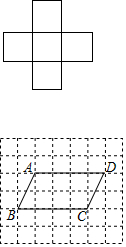
分析 (1)如图3中,取AD中点H,沿CH剪开,①旋转到②的位置即可(△HCD绕点H逆时针旋转180°即可);
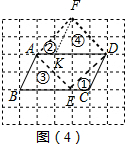
(2)在BC上取一点E,使得CE=1,沿AE、ED剪开,①放到②的位置,③放到④的位置即可;
解答 解:(1)如图3中,取AD中点H,沿CH剪开,①旋转到②的位置即可(△HCD绕点H逆时针旋转180°即可),
△EBC即为等腰三角形(EB=EC=2$\sqrt{5}$).
(2)在BC上取一点E,使得CE=1,沿AE、ED剪开,①放到②的位置,③放到④的位置即可,
正方形AEDF即为所求.
点评 本题考查四边形综合题、复杂作图、等腰三角形的性质、正方形的判定和性质等知识,解题的关键是利用数形结合的思想解决问题,本题考查了学生的动手能力,属于中考常考题型.

练习册系列答案
相关题目
20.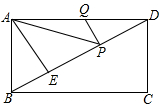 如图,BD为矩形ABCD的对角线,AE⊥BD,垂足为E,tan∠BAE=$\frac{\sqrt{3}}{3}$,BE=1,点P、Q分别在BD、AD上,连接AP、PQ,则AP+PQ的最小值为3.
如图,BD为矩形ABCD的对角线,AE⊥BD,垂足为E,tan∠BAE=$\frac{\sqrt{3}}{3}$,BE=1,点P、Q分别在BD、AD上,连接AP、PQ,则AP+PQ的最小值为3.
 如图,BD为矩形ABCD的对角线,AE⊥BD,垂足为E,tan∠BAE=$\frac{\sqrt{3}}{3}$,BE=1,点P、Q分别在BD、AD上,连接AP、PQ,则AP+PQ的最小值为3.
如图,BD为矩形ABCD的对角线,AE⊥BD,垂足为E,tan∠BAE=$\frac{\sqrt{3}}{3}$,BE=1,点P、Q分别在BD、AD上,连接AP、PQ,则AP+PQ的最小值为3.
5.我国的钓鱼岛面积约为4400000m2,用科学记数法表示为( )
| A. | 4.4×106 | B. | 44×105 | C. | 4×106 | D. | 0.44×107 |
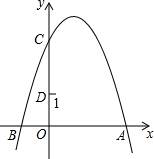 如图,抛物线y=-x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点,若△PCD是以CD为底的等腰三角形,则点P的坐标为(1+$\sqrt{2}$,2)或(1-$\sqrt{2}$,2).
如图,抛物线y=-x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点,若△PCD是以CD为底的等腰三角形,则点P的坐标为(1+$\sqrt{2}$,2)或(1-$\sqrt{2}$,2).
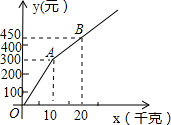 甲、乙两家樱桃采摘园的品质相同,销售价格也相同,“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.
甲、乙两家樱桃采摘园的品质相同,销售价格也相同,“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.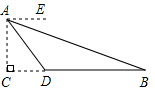 为了测量校园池塘B,D两地之间的距离,从距离地面高度为20米的教学楼A处测得点B的俯角∠EAB=15°,点D的俯角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求池塘B,D两地之间的距离(结果保留整数米).(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)
为了测量校园池塘B,D两地之间的距离,从距离地面高度为20米的教学楼A处测得点B的俯角∠EAB=15°,点D的俯角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求池塘B,D两地之间的距离(结果保留整数米).(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)