题目内容
10.分解因式:9x-x3=x(3+x)(3-x).分析 首先提取公因式x,金进而利用平方差公式分解因式得出答案.
解答 解:原式=x(9-x2)
=x(3-x)(3+x).
故答案为:x(3-x)(3+x).
点评 此题主要考查了提取公因式法以及公式法分解因式,正确运用平方差公式是解题关键.

练习册系列答案
相关题目
20.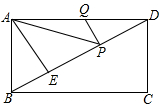 如图,BD为矩形ABCD的对角线,AE⊥BD,垂足为E,tan∠BAE=$\frac{\sqrt{3}}{3}$,BE=1,点P、Q分别在BD、AD上,连接AP、PQ,则AP+PQ的最小值为3.
如图,BD为矩形ABCD的对角线,AE⊥BD,垂足为E,tan∠BAE=$\frac{\sqrt{3}}{3}$,BE=1,点P、Q分别在BD、AD上,连接AP、PQ,则AP+PQ的最小值为3.
 如图,BD为矩形ABCD的对角线,AE⊥BD,垂足为E,tan∠BAE=$\frac{\sqrt{3}}{3}$,BE=1,点P、Q分别在BD、AD上,连接AP、PQ,则AP+PQ的最小值为3.
如图,BD为矩形ABCD的对角线,AE⊥BD,垂足为E,tan∠BAE=$\frac{\sqrt{3}}{3}$,BE=1,点P、Q分别在BD、AD上,连接AP、PQ,则AP+PQ的最小值为3.
1.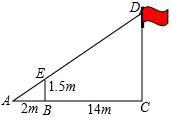 如图,某校数学兴趣小组利用标杆BE测量学校旗杆CD的高度,标杆BE高1.5m,测得AB=2m,BC=14m,则旗杆CD高度是( )
如图,某校数学兴趣小组利用标杆BE测量学校旗杆CD的高度,标杆BE高1.5m,测得AB=2m,BC=14m,则旗杆CD高度是( )
 如图,某校数学兴趣小组利用标杆BE测量学校旗杆CD的高度,标杆BE高1.5m,测得AB=2m,BC=14m,则旗杆CD高度是( )
如图,某校数学兴趣小组利用标杆BE测量学校旗杆CD的高度,标杆BE高1.5m,测得AB=2m,BC=14m,则旗杆CD高度是( )| A. | 9m | B. | 10.5m | C. | 12m | D. | 16m |
18.内角和与外角和相等的多边形是( )
| A. |  | B. |  | C. |  | D. |  |
5.我国的钓鱼岛面积约为4400000m2,用科学记数法表示为( )
| A. | 4.4×106 | B. | 44×105 | C. | 4×106 | D. | 0.44×107 |
2.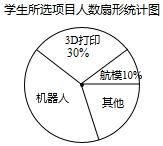 初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
男、女生所选项目人数统计表
根据以上信息解决下列问题:
(1)m=8,n=3;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为144°;
(3)从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.
 初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.男、女生所选项目人数统计表
| 项目 | 男生(人数) | 女生(人数) |
| 机器人 | 7 | 9 |
| 3D打印 | m | 4 |
| 航模 | 2 | 2 |
| 其他 | 5 | n |
(1)m=8,n=3;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为144°;
(3)从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.
19.下列命题是假命题的是( )
| A. | 不在同一直线上的三点确定一个圆 | |
| B. | 角平分线上的点到角两边的距离相等 | |
| C. | 正六边形的内角和是720° | |
| D. | 角的边越大,角就越大 |
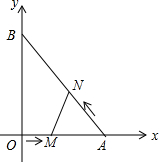 如图,在平面直角坐标系中,直角三角形AOB的顶点A、B分别落在坐标轴上.O为原点,点A的坐标为(6,0),点B的坐标为(0,8).动点M从点O出发.沿OA向终点A以每秒1个单位的速度运动,同时动点N从点A出发,沿AB向终点B以每秒$\frac{5}{3}$个单位的速度运动.当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).
如图,在平面直角坐标系中,直角三角形AOB的顶点A、B分别落在坐标轴上.O为原点,点A的坐标为(6,0),点B的坐标为(0,8).动点M从点O出发.沿OA向终点A以每秒1个单位的速度运动,同时动点N从点A出发,沿AB向终点B以每秒$\frac{5}{3}$个单位的速度运动.当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).