题目内容
9. 抛物线F与x轴相交于A、B两点(点A在点B的左边),对称轴为直线x=1,顶点C在直线y=x-5上,与y轴相交于点D(0,3).
抛物线F与x轴相交于A、B两点(点A在点B的左边),对称轴为直线x=1,顶点C在直线y=x-5上,与y轴相交于点D(0,3).(1)求抛物线F的解析式;
(2)连结CD、BD,则线段BD与CD的数量关系和位置关系分别为BD⊥CD,BD=3CD;
(3)点P为直线CD上方抛物线F上的一个动点,PQ⊥CD,垂足为Q,若∠QPD=∠DBC,求点P的坐标.
分析 (1)先利用一次函数解析式确定顶点C的坐标为(1,-4),再设顶点式y=a(x-1)2-4,然后把D点坐标代入求出a的值即可;
(2)作CH⊥y轴于H,如图1,先判断△OBD为等腰直角三角形得到∠ODB=45°,BD=3$\sqrt{2}$,再判断△CDH为等腰直角三角形得到∠CDH=45°,CD=$\sqrt{2}$,所以BD⊥CD,BD=3CD;
(3)讨论:当点Q在点D在下方时,PD交BC于E点,如图2,利用∠DBC=∠QPD得到∠BCD=∠PDQ,则∠BDE=∠DBE,所以ED=EC=BE,于是可得到E(2,-2),易得直线DE的解析式为y=$\frac{1}{2}$x-3,然后解方程组$\left\{\begin{array}{l}{y=\frac{1}{2}x-3}\\{y={x}^{2}-2x-3}\end{array}\right.$可得P点坐标;当点Q在点D在上方时,如图3,先证明∠DCB=∠QDP,则PD∥BC,易得直线BC的解析式为y=2x-6,利用两直线平行问题可得直线PD的解析式为y=2x-3,然后解方程组$\left\{\begin{array}{l}{y=2x-3}\\{y={x}^{2}-2x-3}\end{array}\right.$得此时P点坐标.
解答 解:(1)将x=1代入y=x-5得y=-4
∴顶点C的坐标为(1,-4)
设y=a(x-1)2-4,
把D(0,-3)代入得a-4=-3,解得a=1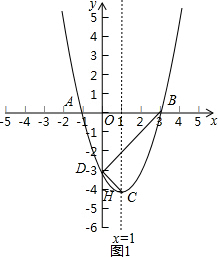
∴抛物线解析式为y=(x-1)2-4,即y=x2-2x-3;
(2)作CH⊥y轴于H,如图1,
∵D(0,-3),B(3,0),
∴OB=OD,
∴△OBD为等腰直角三角形,
∴∠ODB=45°,BD=3$\sqrt{2}$,
∵C(1,-4),
∴CH=DH=1,
∴△CDH为等腰直角三角形,
∴∠CDH=45°,CD=$\sqrt{2}$,
∴∠BDC=90°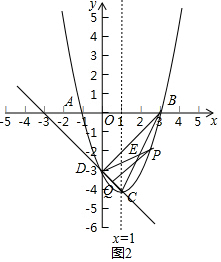
∴BD⊥CD,BD=3CD,
故答案为BD⊥CD,BD=3CD,
(3)①当点Q在点D在下方时,PD交BC于E点,如图2,
∵PQ⊥CD
∴∠PQD=∠BDC=90°
又∵∠DBC=∠QPD,
∴∠BCD=∠PDQ,
∴∠BDE=∠DBE,
∴ED=EC=BE,即E为BC的中点,
∴E(2,-2),
易得直线DE的解析式为y=$\frac{1}{2}$x-3,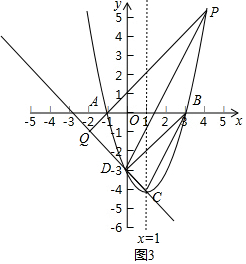
解方程组$\left\{\begin{array}{l}{y=\frac{1}{2}x-3}\\{y={x}^{2}-2x-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=-3}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{5}{2}}\\{y=-\frac{7}{4}}\end{array}\right.$,则此时P点坐标为($\frac{5}{2}$,-$\frac{7}{4}$);
②当点Q在点D在上方时,如图3,
∵∠PQD=∠BDC=90°,∠DBC=∠QPD,
∴∠DCB=∠QDP,
∴PD∥BC,
易得直线BC的解析式为y=2x-6,
∴直线PD的解析式为y=2x-3,
解方程组$\left\{\begin{array}{l}{y=2x-3}\\{y={x}^{2}-2x-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=-3}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=5}\end{array}\right.$,则此时P点坐标为(4,5);
综上所述,点P的坐标为($\frac{5}{2}$,-$\frac{7}{4}$),(4,5).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和等腰直角三角形的性质;会利用待定系数法求函数解析式,会通过解方程组求二次函数与一次函数的交点坐标;理解坐标与图形性质;会应用分类讨论的思想解决数学问题.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案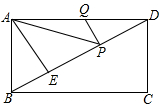 如图,BD为矩形ABCD的对角线,AE⊥BD,垂足为E,tan∠BAE=$\frac{\sqrt{3}}{3}$,BE=1,点P、Q分别在BD、AD上,连接AP、PQ,则AP+PQ的最小值为3.
如图,BD为矩形ABCD的对角线,AE⊥BD,垂足为E,tan∠BAE=$\frac{\sqrt{3}}{3}$,BE=1,点P、Q分别在BD、AD上,连接AP、PQ,则AP+PQ的最小值为3. | 红球1 | 红球2 | 红球3 | 白球1 | 白球2 | |
| 红球1 | (红1,红2) | (红1,红3) | (红1,白1) | (红1,白2) | |
| 红球2 | (红2,红3) | (红2,白1) | (红2,白2) | ||
| 红球3 | (红3,白1) | (红3,白2) | |||
| 白球1 | (白1,白2) | ||||
| 白球2 |
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{2}{5}$ |
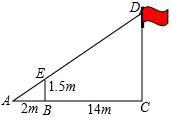 如图,某校数学兴趣小组利用标杆BE测量学校旗杆CD的高度,标杆BE高1.5m,测得AB=2m,BC=14m,则旗杆CD高度是( )
如图,某校数学兴趣小组利用标杆BE测量学校旗杆CD的高度,标杆BE高1.5m,测得AB=2m,BC=14m,则旗杆CD高度是( )| A. | 9m | B. | 10.5m | C. | 12m | D. | 16m |
| A. |  | B. |  | C. |  | D. |  |
| A. | 不在同一直线上的三点确定一个圆 | |
| B. | 角平分线上的点到角两边的距离相等 | |
| C. | 正六边形的内角和是720° | |
| D. | 角的边越大,角就越大 |
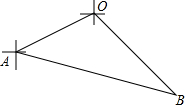 如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时10海里的速度航行,甲沿南偏西75°方向以每小时10$\sqrt{2}$海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为10+10$\sqrt{3}$海里/小时?
如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时10海里的速度航行,甲沿南偏西75°方向以每小时10$\sqrt{2}$海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为10+10$\sqrt{3}$海里/小时?