题目内容
当k为何值时,方程x2-(k+1)x+(k-2)=0的根满足下列条件:
(1)两根互为相反数;
(2)两根互为倒数;
(3)有一根为0,另一根不为0.
(1)两根互为相反数;
(2)两根互为倒数;
(3)有一根为0,另一根不为0.
考点:根与系数的关系
专题:计算题
分析:(1)根据根与系数的关系x1+x2=0得到k+1=0,然后解关于k的方程即可;
(2)根据根与系数的关系x1•x2=1得到k-2=1,然后解关于k的方程即可;
(3)根据根与系数的关系x1•x2=0得到k-2=0,然后解关于k的方程即可.
(2)根据根与系数的关系x1•x2=1得到k-2=1,然后解关于k的方程即可;
(3)根据根与系数的关系x1•x2=0得到k-2=0,然后解关于k的方程即可.
解答:解:(1)根据题意得k+1=0,解得k=-1;
(2)根据题意得k-2=1,解得k=3;
(3)根据题意得k+1≠0且k-2=0,解得k=2.
(2)根据题意得k-2=1,解得k=3;
(3)根据题意得k+1≠0且k-2=0,解得k=2.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
 如图,已知正比例函数和反比例函数的图象都经过点A(3,3).
如图,已知正比例函数和反比例函数的图象都经过点A(3,3).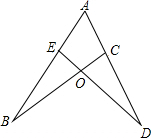 如图,已知AB=AD,BO=DO,求证:AE=AC.
如图,已知AB=AD,BO=DO,求证:AE=AC.