题目内容
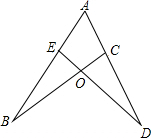 如图,已知AB=AD,BO=DO,求证:AE=AC.
如图,已知AB=AD,BO=DO,求证:AE=AC.考点:全等三角形的判定与性质
专题:证明题
分析:连接BD,由AB=AD,BO=DO,利用等边对等角得到两对角相等,利用等式的性质得到∠ABC=∠ADE,再由∠A为公共角,AB=AD,利用ASA得到三角形ABC与三角形ADE全等,利用全等三角形对应边相等即可得证.
解答: 证明:连接BD,
证明:连接BD,
∵AB=AD,BO=DO,
∴∠ABD=∠ADB,∠OBD=∠ODB,
∴∠ABD-∠OBD=∠ADB-∠ODB,即∠ABC=∠ADE,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(ASA),
∴AC=AE.
 证明:连接BD,
证明:连接BD,∵AB=AD,BO=DO,
∴∠ABD=∠ADB,∠OBD=∠ODB,
∴∠ABD-∠OBD=∠ADB-∠ODB,即∠ABC=∠ADE,
在△ABC和△ADE中,
|
∴△ABC≌△ADE(ASA),
∴AC=AE.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
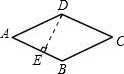 如图,已知菱形ABCD的边长是2,DE⊥AB,垂足为E,∠A=45°,求菱形ABCD的面积.
如图,已知菱形ABCD的边长是2,DE⊥AB,垂足为E,∠A=45°,求菱形ABCD的面积. 如图,一个足球是用黑、白两种颜色的皮块缝制而成的,黑皮块是正五边形,白皮块是正六边形,黑、白皮块数目比为3:5,若黑皮和白皮一共48块,则白皮有
如图,一个足球是用黑、白两种颜色的皮块缝制而成的,黑皮块是正五边形,白皮块是正六边形,黑、白皮块数目比为3:5,若黑皮和白皮一共48块,则白皮有