Question

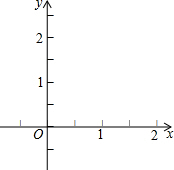如图，在平面直角坐标系中，点A₁，A₂在x轴上，点B₁，B₂在y轴上，其坐标分别为A₁（1，0），A₂（2，0），B₁（0，1），B₂（0，2）
（1）只用直尺和圆规作出∠A₁OB₁的平分线（保留作图痕迹），作出的平分线上有点P的坐标为（2a，b+1），则写出a与b的数量关系．
（2）分别以A₁A₂B₁B₂其中的任意两点与点O为顶点作三角形，是等腰三角形的概率．

Answer 1

考点：作图—基本作图,坐标与图形性质,等腰三角形的判定,概率公式

专题：

分析：（1）首先根据角平分线的做法作图即可；根据角平分线的性质：角平分线上的点到角两边的距离相等可得2a=b+1，整理可得答案；
（2）首先找出以A₁A₂B₁B₂其中的任意两点与点O为顶点所组成的三角形个数，然后再找出等腰三角形的个数，再利用概率公式算出概率．

解答：解：（1）如图所示：
∵OM平分∠A₁OB₁，点P的坐标为（2a，b+1），
∴2a=b+1，
∴b=2a-1；

（2）以A₁A₂B₁B₂其中的任意两点与点O为顶点作三角形，能作4个，
其中A₁B₁O，A₂B₂O为等腰三角形，共2个，
故概率为：0.5．

点评：此题主要考查了学生作一个角平分线的基本作图方法，角平分线的性质，会对等腰三角形作出判断，概率．关键是掌握角平分线的性质．