题目内容
 已知:如图,在Rt△ABC中,∠A=90°,AB=AC=1,P是AB边上不与A点、B点重合的任意一个动点,PQ⊥BC于点Q,QR⊥AC于点R.
已知:如图,在Rt△ABC中,∠A=90°,AB=AC=1,P是AB边上不与A点、B点重合的任意一个动点,PQ⊥BC于点Q,QR⊥AC于点R.(1)求证:PQ=BQ;
(2)设BP=x,CR=y,求y关于x的函数解析式,并写出定义域;
(3)当x为何值时,PR∥BC.
考点:等腰直角三角形
专题:
分析:(1)由已知条件可证得△BPQ为等腰直角三角形,从而证得PQ=BQ.
(2)根据题意证三角形BPQ和三角形CQR都是等腰直角三角形,得到CQ和BQ的和等于BC,从而得到y与x的关系.
(3)因为PR∥BC,从而得到△APR和△ABC相似,对应线段成比例,得到x的值.
(2)根据题意证三角形BPQ和三角形CQR都是等腰直角三角形,得到CQ和BQ的和等于BC,从而得到y与x的关系.
(3)因为PR∥BC,从而得到△APR和△ABC相似,对应线段成比例,得到x的值.
解答:(1)证明:∵∠A=90°,AB=AC=1
∴∠B=∠C=45°
又∵PQ⊥BQ
∴∠BPQ=45°
∴△BPQ是等腰三角形
∴PQ=BQ.
(2)解:在等腰直角△BPQ中,
∵BP=x
∴BQ=
x
在Rt△ABC中,BC=
=
=
在等腰直角三角形CQR中,CR=y
∴CQ=
y
∵CQ=BC-BQ
即
y=
-
x
所以y=-
x+1.
(3)解:∵PR∥BC,PQ⊥BC
∴PR⊥PQ
又∵△BPQ为等腰三角形,
∴PQ=
x
∵PR∥BC
∴∠PRQ=∠RQC=45°
∴PR=
x
∠A=∠A,∠APR=∠B,∠ARP=∠C
∴△APR∽△ABC
∴
=
即
=
解得:x=
.

∴∠B=∠C=45°
又∵PQ⊥BQ
∴∠BPQ=45°
∴△BPQ是等腰三角形
∴PQ=BQ.
(2)解:在等腰直角△BPQ中,
∵BP=x
∴BQ=
| ||
| 2 |
在Rt△ABC中,BC=
| AB2+BC2 |
| 1+1 |
| 2 |
在等腰直角三角形CQR中,CR=y
∴CQ=
| 2 |
∵CQ=BC-BQ
即
| 2 |
| 2 |
| ||
| 2 |
所以y=-
| 1 |
| 2 |
(3)解:∵PR∥BC,PQ⊥BC
∴PR⊥PQ
又∵△BPQ为等腰三角形,
∴PQ=
| ||
| 2 |
∵PR∥BC
∴∠PRQ=∠RQC=45°
∴PR=
| ||
| 2 |
∠A=∠A,∠APR=∠B,∠ARP=∠C
∴△APR∽△ABC
∴
| PR |
| BC |
| PA |
| AB |
即
| ||||
| 2 |
| 1-x |
| 1 |
解得:x=
| 2 |
| 3 |

点评:考查了等腰直角三角形的性质,以及相似三角形的性质,根据对应线段成比例来解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在平面直角坐标系中,点A1,A2在x轴上,点B1,B2在y轴上,其坐标分别为A1(1,0),A2(2,0),B1(0,1),B2(0,2)
如图,在平面直角坐标系中,点A1,A2在x轴上,点B1,B2在y轴上,其坐标分别为A1(1,0),A2(2,0),B1(0,1),B2(0,2)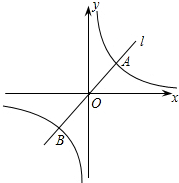 我们知道,y=x的图象向右平移1个单位得到y=x-1的图象,类似的,y=
我们知道,y=x的图象向右平移1个单位得到y=x-1的图象,类似的,y= 任意抛掷一枚均匀的骰子(各个面上的点数为1-6),将第一次,第二次抛掷的点数分别记为m,n
任意抛掷一枚均匀的骰子(各个面上的点数为1-6),将第一次,第二次抛掷的点数分别记为m,n 如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为
如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为 如图,已知坐标平面内有两点A(1,0),B(-2,4),现将AB绕着点A顺时针旋转90°至AC位置,则点C的坐标为
如图,已知坐标平面内有两点A(1,0),B(-2,4),现将AB绕着点A顺时针旋转90°至AC位置,则点C的坐标为 将一个有45°角的三角板的直角顶点放在一张宽为5cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的周长为
将一个有45°角的三角板的直角顶点放在一张宽为5cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的周长为