题目内容
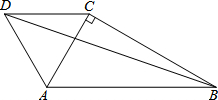 如图,在△ABC中,∠ACB=90°,∠ABC=30°,BC=2
如图,在△ABC中,∠ACB=90°,∠ABC=30°,BC=2| 3 |
(1)求四边形ABCD的面积;
(2)求BD的长.
考点:解直角三角形,等边三角形的性质,勾股定理
专题:
分析:(1)先解直角△ABC,得出AC=2,AB=4,则△ABC的面积=
AC•BC=2
.再过点D作DE⊥AC于E,解直角△ADE,得出DE=
,则△ACD的面积=
AC•DE=
,则根据四边形ABCD的面积=△ABC的面积+△ACD的面积求解;
(2)过点D作DF⊥AB于F.先求出∠DAF=180°-∠BAC-∠DAC=60°,再解直角△ADF,得出AF=1,DF=
,则BF=AF+AB=5,然后在直角△BDF中运用勾股定理即可求出BD的长度.
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
(2)过点D作DF⊥AB于F.先求出∠DAF=180°-∠BAC-∠DAC=60°,再解直角△ADF,得出AF=1,DF=
| 3 |
解答: 解:(1)∵在△ABC中,∠ACB=90°,∠ABC=30°,BC=2
解:(1)∵在△ABC中,∠ACB=90°,∠ABC=30°,BC=2
,
∴AC=2,AB=4.
∴△ABC的面积=
AC•BC=
×2×2
=2
.
∵△ACD为等边三角形,
∴AD=AC=2,∠DAC=60°.
过点D作DE⊥AC于E.
在△ADE中,∵∠AED=90°,∠DAE=60°,AD=2,
∴DE=AD•sin∠DAE=2×
=
,
∴△ACD的面积=
AC•DE=
×2×
=
,
∴四边形ABCD的面积=△ABC的面积+△ACD的面积=2
+
=3
;
(2)过点D作DF⊥AB于F.
∵∠BAC=60°,∠DAC=60°,
∴∠DAF=180°-∠BAC-∠DAC=60°.
在△ADF中,∠AFD=90°,∠DAF=60°,AD=2,
∴AF=1,DF=
,
∴BF=AF+AB=1+4=5,
∴BD=
=
=2
.
 解:(1)∵在△ABC中,∠ACB=90°,∠ABC=30°,BC=2
解:(1)∵在△ABC中,∠ACB=90°,∠ABC=30°,BC=2| 3 |
∴AC=2,AB=4.
∴△ABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∵△ACD为等边三角形,
∴AD=AC=2,∠DAC=60°.
过点D作DE⊥AC于E.
在△ADE中,∵∠AED=90°,∠DAE=60°,AD=2,
∴DE=AD•sin∠DAE=2×
| ||
| 2 |
| 3 |
∴△ACD的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴四边形ABCD的面积=△ABC的面积+△ACD的面积=2
| 3 |
| 3 |
| 3 |
(2)过点D作DF⊥AB于F.
∵∠BAC=60°,∠DAC=60°,
∴∠DAF=180°-∠BAC-∠DAC=60°.
在△ADF中,∠AFD=90°,∠DAF=60°,AD=2,
∴AF=1,DF=
| 3 |
∴BF=AF+AB=1+4=5,
∴BD=
| BF2+DF2 |
52+(
|
| 7 |
点评:本题考查了解直角三角形,三角形的面积,勾股定理,难度适中.准确作出辅助线构造直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将点A(-3,-1)向上平移3个单位得到点B,则点B所在的象限是( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图,在平面直角坐标系中,点A1,A2在x轴上,点B1,B2在y轴上,其坐标分别为A1(1,0),A2(2,0),B1(0,1),B2(0,2)
如图,在平面直角坐标系中,点A1,A2在x轴上,点B1,B2在y轴上,其坐标分别为A1(1,0),A2(2,0),B1(0,1),B2(0,2) 如图,△ABC中,AD⊥BC,垂足为D,DE平分∠ADB,交AB于E,∠C=∠DAC,DE与CA平行吗?为什么?
如图,△ABC中,AD⊥BC,垂足为D,DE平分∠ADB,交AB于E,∠C=∠DAC,DE与CA平行吗?为什么?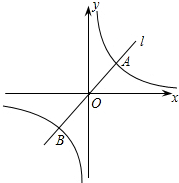 我们知道,y=x的图象向右平移1个单位得到y=x-1的图象,类似的,y=
我们知道,y=x的图象向右平移1个单位得到y=x-1的图象,类似的,y= 如图,已知坐标平面内有两点A(1,0),B(-2,4),现将AB绕着点A顺时针旋转90°至AC位置,则点C的坐标为
如图,已知坐标平面内有两点A(1,0),B(-2,4),现将AB绕着点A顺时针旋转90°至AC位置,则点C的坐标为