题目内容

如图，小明用一块有一个锐角为30°的直角三角板测量树高，已知小明离树的距离为4米，DE为1.68米，那么这棵树大约有多高？（精确到0.1米）
考点：解直角三角形的应用
专题：
分析：因为∠CAD=30°，则AC=2CD，再利用勾股定理求得CD的长，再加上DE的长就求出了树的高度．
解答：解：在Rt△ACD中，∠CAD=30°，AD=4m，
设CD=x，则AC=2x，由AD2+CD2=AC2，
得，42+x2=4x2，
解得：x=
4
3
3
≈2.3，
∴2.3+1.68≈4.0（m），
答：故大树高为4.0米．
点评：本题中主要是利用三角函数解决直角梯形的问题，直角梯形可以通过作高转化为直角三角形的问题．
练习册系列答案
相关题目
如果两块面积为a公顷、b公顷的棉田，分别产棉花m千克、n千克，那么这两块棉田的平均产量为（　　）
A、
m
a
千克/公顷
B、
n
b
千克/公顷
C、
m+n
a+b
千克/公顷
D、
m
a
+
n
b
千克/公顷
将点A（-3，-1）向上平移3个单位得到点B，则点B所在的象限是（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
（1）如图1，四边形ABCD是矩形，E为AD上一点，且BE=ED，P为对角线BD上一点，PF⊥BE于点F，PG⊥AD于点G．判断PF、PG和AB的数量关系并说明理由．
（2）如图2，当四边形ABCD变为平行四边形，其他条件不变，若∠ABC=60°，判断PF、PG和AB的数量关系并说明理由．
（3）如图3，当四边形ABCD满足∠ABD=90°，AB=3，BD=4，其它条件不变，判断PF、PG和AB的数量关系并说明理由．
解不等式组：
2x-1≤x
2(x+1)≥-1
，并将解集在数轴上表示出来．
（1）计算：|-1|-2tan45°-（-
4
）；
（2）解不等式：x＞
1
2
x+1．
如图，在平面直角坐标系中，点A1，A2在x轴上，点B1，B2在y轴上，其坐标分别为A1（1，0），A2（2，0），B1（0，1），B2（0，2）
（1）只用直尺和圆规作出∠A1OB1的平分线（保留作图痕迹），作出的平分线上有点P的坐标为（2a，b+1），则写出a与b的数量关系．
（2）分别以A1A2B1B2其中的任意两点与点O为顶点作三角形，是等腰三角形的概率．
在平面直角坐标系中，反比例函数与二次函数y=k（x2+x-1）的图象交于点A（1，k）和点B（-1，-k）．
（1）当k=-2时，求反比例函数的解析式；
（2）已知经过原点O的两条直线AB与CD分别与双曲线y=
k
x
（k＞0）交于A、B和C、D，那么AB与CD互相平分，所以四边形ACBD是平行四边形．问：平行四边形ABCD能否成为矩形？能否成为正方形？若能，请说明直线AB、CD的位置关系；若不能，请说明理由；
（3）设二次函数的图象的顶点为Q，当△ABQ是以AB为斜边的直角三角形时，求k的值．
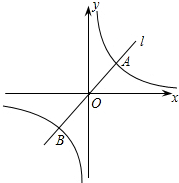我们知道，y=x的图象向右平移1个单位得到y=x-1的图象，类似的，y=
k
x
（k≠0）的图象向左平移2个单位得到y=
k
x+2
（k≠0）的图象．请运用这一知识解决问题．
如图，已知反比例函数y=
2
x
的图象C与正比例函数y=ax（a≠0）的图象l相交于点A（1，m）和点B．
（1）写出点B的坐标，并求a的值；
（2）将函数y=
2
x
的图象和直线AB同时向右平移n（n＞0）个单位长度，得到的图象分别记为C1和l1，已知图象C1经过点M（3，2）．
①分别写出平移后的两个图象C1和l1对应的函数关系式；
②直接写出不等式
2
x-2
+4≤ax的解集．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网