题目内容
9. 如图,点A(2,n)在反比例函数y=$\frac{3}{x}$的图象上,点B在第二象限,∠AOB=90°,∠OBA=30°,在小组合作学习中,四位同学发现并提出了以下四个结论,其中正确的有( )个.
如图,点A(2,n)在反比例函数y=$\frac{3}{x}$的图象上,点B在第二象限,∠AOB=90°,∠OBA=30°,在小组合作学习中,四位同学发现并提出了以下四个结论,其中正确的有( )个.聪聪:在反比例函数y=$\frac{3}{x}$的图象上任取一个点P,作两坐标轴的垂线,则它们与两坐标轴围成的四边形面积为3;
明明:若直线OA的函数解析式为y=kx,则不等式$\frac{3}{x}$>kx的解集为0<x<2;
智智:过点B的反比例函数的解析式为y=-$\frac{3\sqrt{3}}{x}$;
慧慧:若点D(2+$\frac{3}{2}\sqrt{3}$,$\frac{3}{2}-2\sqrt{3}$),则以点A,O,B,D为顶点的四边形是一个中心对称图形.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由反比例函数系数k的几何意义可知聪聪的话正确;由反比例函数的对称性可找出直线OA与反比例函数的另一个交点坐标,结合函数图象可得出不等式$\frac{3}{x}$>kx的解集,从而判断出明明的话不正确;由点A在反比例函数y=$\frac{3}{x}$的图象上,可求出n的值,从而得出A点的坐标,设点B的坐标为(x,y),结合给定的边角关系可找出关于x、y的二元二次方程组,结合点B的位置可得出点B的坐标,利用待定系数法即可求出过点B的反比例函数的解析式为y=-$\frac{9}{x}$,由此得出智智的话不正确;由A、O、B、D的坐标特征,可得出DA⊥OA,即OB∥DA,结合两点间的距离公式得出OB=DA,由此判断出以点A,O,B,D为顶点的四边形是平行四边形,即慧慧的话正确.综上即可得出结论.
解答 解:∵在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|,
∴聪聪的话正确;
∵点A(2,n),反比例函数的对称性可知:
在第三象限直线OA与反比例函数y=$\frac{3}{x}$有另一个交点(-2,-n),
结合函数图象可知:不等式$\frac{3}{x}$>kx的解集为x<-2,或0<x<2,
∴明明的话不正确;
∵点A(2,n)在反比例函数y=$\frac{3}{x}$的图象上,
∴n=$\frac{3}{2}$,即点A的坐标为(2,$\frac{3}{2}$).
设点B的坐标为(x,y),过点B的反比例函数解析式为y=$\frac{m}{x}$,
则OA=$\sqrt{{2}^{2}+(\frac{3}{2})^{2}}$=$\frac{5}{2}$,OB=$\sqrt{{x}^{2}+{y}^{2}}$=$\frac{OA}{cot∠OBA}$=$\frac{5}{2}\sqrt{3}$,
结合已知可得:$\left\{\begin{array}{l}{\frac{y}{x}•\frac{3}{4}=-1}\\{{x}^{2}+{y}^{2}=\frac{75}{4}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=-\frac{3\sqrt{3}}{2}}\\{y=2\sqrt{3}}\end{array}\right.$.
∴点B的坐标为(-$\frac{3\sqrt{3}}{2}$,2$\sqrt{3}$).
∵点B在反比例函数y=$\frac{m}{x}$的图象上,
∴2$\sqrt{3}$=$\frac{m}{-\frac{3\sqrt{3}}{2}}$,解得:m=-9.
∴过点B的反比例函数的解析式为y=-$\frac{9}{x}$,
∴智智的话不正确;
∵$\frac{\frac{3}{2}-(\frac{3}{2}-2\sqrt{3})}{2-(2+\frac{3}{2}\sqrt{3})}$=-$\frac{4}{3}$,-$\frac{4}{3}$×$\frac{\frac{3}{2}}{2}$=-1,
∴DA⊥OA,
∴AD∥BO.
∵AD=$\sqrt{(2+\frac{3}{2}\sqrt{3}-2)^{2}+(\frac{3}{2}-2\sqrt{3}-\frac{3}{2})^{2}}$=$\frac{5}{2}\sqrt{3}$=OB,
∴以点A,O,B,D为顶点的四边形为平行四边形,
∴以点A,O,B,D为顶点的四边形是一个中心对称图形,
即慧慧的话正确.
综上可知:聪聪和慧慧的话正确.
故选B.
点评 本题考查了反比例函数的性质、待定系数法求函数解析式、两直线垂直的性质、两点间的距离公式以及平行四边形的判定定理,解题的关键是根据给定条件逐条分析四种说法.本题属于中档题,难度不大,但非常繁琐,尤其在断定智智慧慧的话时,结合了多项知识点才得出结论,因此在日常的练习中,应加强知识间联系的练习.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案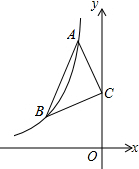 如图:已知点A、B是反比例函数y=-$\frac{6}{x}$上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为2$\sqrt{5}$.
如图:已知点A、B是反比例函数y=-$\frac{6}{x}$上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为2$\sqrt{5}$. | A. | a<1 | B. | a>1 | C. | a≤1 | D. | a≥1 |
| 金额 | 50元 | 60元 | 70元 | 80元 | 90元 | 100元 |
| 居民数 | 200 | 400 | 450 | 500 | 300 | 150 |
| A. | 60,60 | B. | 70,60 | C. | 70,80 | D. | 60,80 |
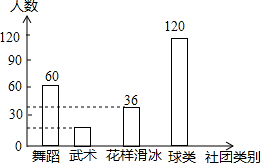 某校开展社团活动,准备组件舞蹈、武术、球类(足球、篮球、乒乓球、羽毛球).花样滑冰四类社团,为了解在校学生对这4个社团活动的喜爱情况,学校随机抽取部分学生进行了“你最喜爱的社团”调查,依据相关数据绘制以下的统计图表,请根据图表中的信息解答下列问题:
某校开展社团活动,准备组件舞蹈、武术、球类(足球、篮球、乒乓球、羽毛球).花样滑冰四类社团,为了解在校学生对这4个社团活动的喜爱情况,学校随机抽取部分学生进行了“你最喜爱的社团”调查,依据相关数据绘制以下的统计图表,请根据图表中的信息解答下列问题:“你最喜爱的社团”调查统计图表
| 社团类别 | 人数 | 占总人数的比例 |
| 舞蹈 | 60 | 25% |
| 武术 | m | 10% |
| 花样滑冰 | 36 | n% |
| 球类 | 120 | 50% |
(2)被调查喜爱球类的学生中有12人最喜爱乒乓球,若该校有2600名学生,试估计全校最喜爱乒乓球的人数.
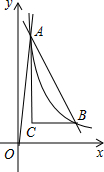 如图,在平面直角坐标系xOy中,正比例函数y=10x与反比例函数y=$\frac{k}{x}$交于点A,点A的横坐标为$\frac{1}{2}$,反比例函数y=$\frac{k}{x}$图象上有一点B,过点B作BC∥x轴,过点A作AC⊥BC,垂足为点C.
如图,在平面直角坐标系xOy中,正比例函数y=10x与反比例函数y=$\frac{k}{x}$交于点A,点A的横坐标为$\frac{1}{2}$,反比例函数y=$\frac{k}{x}$图象上有一点B,过点B作BC∥x轴,过点A作AC⊥BC,垂足为点C.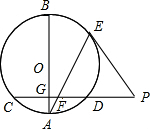 如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G、E是劣弧BD上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.
如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G、E是劣弧BD上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.