题目内容
6.观察下列各式及其验证过程:①2$\sqrt{\frac{2}{3}}$=$\sqrt{2+\frac{2}{3}}$;②3$\sqrt{\frac{3}{8}}$=$\sqrt{3+\frac{3}{8}}$•; ③4$\sqrt{\frac{4}{15}}$=$\sqrt{4+\frac{4}{15}}$; …
第①、②的验证:2$\sqrt{\frac{2}{3}}=\sqrt{\frac{2^3}{3}}=\sqrt{\frac{{{2^3}-2+2}}{3}}=\sqrt{\frac{{2({2^2}-1)+2}}{3}}=\sqrt{\frac{{2({2^2}-1)+2}}{{{2^2}-1}}}=\sqrt{2+\frac{2}{{{2^2}-1}}}=\sqrt{2+\frac{2}{3}}$;3$\sqrt{\frac{3}{8}}=\sqrt{\frac{3^3}{8}}=\sqrt{\frac{{{3^3}-3+3}}{8}}=\sqrt{\frac{{3({3^2}-1)+3}}{8}}=\sqrt{\frac{{3({3^2}-1)+3}}{{{3^2}-1}}}=\sqrt{3+\frac{3}{{{3^2}-1}}}=\sqrt{3+\frac{3}{8}}$•
(1)根据上面的结论和验证过程,猜想5$\sqrt{\frac{5}{24}}$的结果并写出验证过程;
(2)根据对上述各式规律,直接写出第n个等式(不要验证).
分析 (1)根据已知中二次根式的化简即可得出答案.
(2)利用(1)中计算结果,即可得出二次根式的变化规律,进而得出答案即可.
解答 解:(1)5$\sqrt{\frac{5}{24}}$=$\sqrt{5+\frac{5}{24}}$.
5$\sqrt{\frac{5}{24}}$
=$\sqrt{\frac{{5}^{3}}{24}}$,
=$\sqrt{\frac{{5}^{3}-5+5}{24}}$,
=$\sqrt{\frac{5{(5}^{2}-1)+5}{{5}^{2}-1}}$,
=$\sqrt{5+\frac{5}{{5}^{2}-1}}$,
=$\sqrt{5+\frac{5}{24}}$;
(2)n$\sqrt{\frac{n}{{n}^{2}-1}}$=$\sqrt{n+\frac{n}{{n}^{2}-1}}$(n为正整数,n≥2).
点评 此题主要考查了数字变化规律,根据已知得出根式内外变化规律是解题关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
17.一个三角形的三个内角之比是2:3:4,则此三角形为( )
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 以上三种都有可能 |
 如图,直线y1=-x+1与双曲线y2=$\frac{k}{x}$ 交于A,B两点,过A作AC垂直于x轴,△ACO的面积为3,现有下面结论:①k=6;②当x>0时,y1>y2;③若B点坐标为(a,b),则$\sqrt{a+b}$=1;④若B点坐标为(a,b),则$\frac{b}{a}+\frac{a}{b}=-\frac{13}{6}$,其中正确的结论有③④(写出所有正确结论的序号即可).
如图,直线y1=-x+1与双曲线y2=$\frac{k}{x}$ 交于A,B两点,过A作AC垂直于x轴,△ACO的面积为3,现有下面结论:①k=6;②当x>0时,y1>y2;③若B点坐标为(a,b),则$\sqrt{a+b}$=1;④若B点坐标为(a,b),则$\frac{b}{a}+\frac{a}{b}=-\frac{13}{6}$,其中正确的结论有③④(写出所有正确结论的序号即可).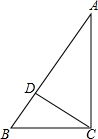 如图,CD是AB上的高,AC=4,BC=3,DB=$\frac{9}{5}$
如图,CD是AB上的高,AC=4,BC=3,DB=$\frac{9}{5}$