题目内容
15.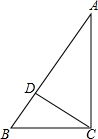 如图,CD是AB上的高,AC=4,BC=3,DB=$\frac{9}{5}$
如图,CD是AB上的高,AC=4,BC=3,DB=$\frac{9}{5}$(1)求CD的长.
(2)求AD的长.
(3)判断△ABC的形状,并说明理由.
分析 (1)由CD是AB上的高,得到三角形BCD为直角三角形,由BC与DB,利用勾股定理求出CD的长;
(2)由CD是AB上的高,得到三角形ACD为直角三角形,由AC与CD,利用勾股定理求出AD的长;
(3)三角形ABC为直角三角形,理由为:由BD+AD求出AB的长,利用勾股定理的逆定理得到三角形ABC为直角三角形.
解答  解:(1)∵CD是AB上的高,BC=3,DB=$\frac{9}{5}$,
解:(1)∵CD是AB上的高,BC=3,DB=$\frac{9}{5}$,
∴CD=$\sqrt{B{C}^{2}-B{D}^{2}}$=$\sqrt{9-\frac{81}{25}}$=$\frac{12}{5}$;
(2)∵CD是AB上的高,AC=4,CD=$\frac{12}{5}$,
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{16-\frac{144}{25}}$=$\frac{16}{5}$;
(3)△ABC是直角三角形.理由是:
∵AB=BD+AD=$\frac{9}{5}$+$\frac{16}{5}$=5,
又∵AC=4,BC=3,
∴AC2+BC2=AB2,
∴△ABC为直角三角形.
点评 此题主要考查了勾股定理和勾股定理逆定理,关键是掌握在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方;三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
相关题目
3.2015年“五.四青年节”我校举行八年级文艺表演,表演的舞台是面积约为73平方米的一个正方形.试估计该舞台的边长的大小在( )米.
| A. | $\sqrt{8}$与$\sqrt{9}$之间 | B. | 6与7之间 | C. | 7与8之间 | D. | 8与9之间 |
 如图,A、B是⊙O上两点,有下列四种寻找$\widehat{AB}$的中点C的方法:
如图,A、B是⊙O上两点,有下列四种寻找$\widehat{AB}$的中点C的方法:
 如图,将边长为2的正方形ABCD沿对角线AC平移至正方形A1B1C1D1,当重叠部分面积为2时,则正方形ABCD平移的距离AA1=2$\sqrt{2}$-2.
如图,将边长为2的正方形ABCD沿对角线AC平移至正方形A1B1C1D1,当重叠部分面积为2时,则正方形ABCD平移的距离AA1=2$\sqrt{2}$-2.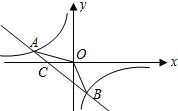 如图,已知A(-4,n),B(2,-4)是一次函数y1=kx+b的图象和反比例函数y2=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,n),B(2,-4)是一次函数y1=kx+b的图象和反比例函数y2=$\frac{m}{x}$的图象的两个交点. 已知,如图所示,折叠矩形的一边AD,使点D落在BC边的点F处,如果AB=8cm,BC=10cm
已知,如图所示,折叠矩形的一边AD,使点D落在BC边的点F处,如果AB=8cm,BC=10cm