题目内容
1.(1)如图(1),E为平行四边形ABCD内一点,求证:S△ADE+S△BCE=S△ABE+S△DCE;(2)如图(2),若点E在平行四边形ABCD边CD所在直线上方,请探究S△ADE、S△BCE、S△ABE、S△DCE之间的数量关系.
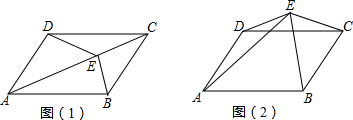
分析 (1)作EM⊥CD 于M,直线EM交AB于点N,根据平行线的性质得到EN⊥AB,根据三角形的面积公式得到S△ABE=$\frac{1}{2}$AB•EN,S△CDE=$\frac{1}{2}$CD•EM,于是得到S△ABE+S△CDE=$\frac{1}{2}$AB(EM+EN)=$\frac{1}{2}$AB•MN=$\frac{1}{2}$S四边形ABCD,同理S△ADE+S△BCE=$\frac{1}{2}$S四边形ABCD,等量代换得到结论;
(2)过E作EF⊥AB于点F,交CD于点G. 于是得到S△ABE=$\frac{1}{2}$AB•EG+$\frac{1}{2}$AB•GF=$\frac{1}{2}$ S平行四边形ABCD+$\frac{1}{2}$AB•EG,由于S△CDE=$\frac{1}{2}$CD•EG,S△ABG=$\frac{1}{2}$S平行四边形ABCD,等量代换得到结论.
解答 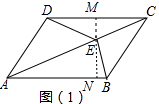 证明:(1)如图(1),作EM⊥CD 于M,直线EM交AB于点N,
证明:(1)如图(1),作EM⊥CD 于M,直线EM交AB于点N,
∵AB‖CD,
∴EN⊥AB,
∴S△ABE=$\frac{1}{2}$AB•EN,S△CDE=$\frac{1}{2}$CD•EM,
∵AB=CD,
∴S△ABE+S△CDE=$\frac{1}{2}$AB(EM+EN)=$\frac{1}{2}$AB•MN=$\frac{1}{2}$S四边形ABCD,同理S△ADE+S△BCE=$\frac{1}{2}$S四边形ABCD,
∴S△ADE+S△BCE=S△ABE+S△DCE;
(2)如图(2),过E作EF⊥AB于点F,交CD于点G.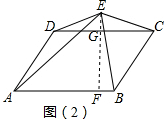 则S△ABE=$\frac{1}{2}$AB•EF
则S△ABE=$\frac{1}{2}$AB•EF
=$\frac{1}{2}$AB•(EG+GF)
=$\frac{1}{2}$AB•EG+$\frac{1}{2}$AB•GF
=$\frac{1}{2}$ S平行四边形ABCD+$\frac{1}{2}$AB•EG,
又∵S△CDE=$\frac{1}{2}$CD•EG,S△ABG=$\frac{1}{2}$S平行四边形ABCD,
∴S△ABE+S△CDE=$\frac{1}{2}$S平行四边形ABCD.
∴S△ABE=S△ADE+S△CDE+S△BCE.
点评 本题考查了平行四边形的性质.平行四边形的面积和三角形的面积的求法,熟记三角形的面积公式是解题的关键.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案| A. | 2.5cm | B. | 2.4cm | C. | 5cm | D. | 3cm |
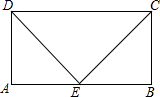 已知:如图,在?ABCD中,E是AB的中点,ED=EC,求证:四边形ABCD是矩形.
已知:如图,在?ABCD中,E是AB的中点,ED=EC,求证:四边形ABCD是矩形.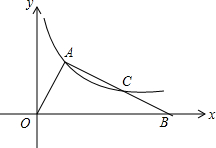 如图,直角△AOB的斜边OB在x轴正半轴上,双曲线y=$\frac{k}{x}$(x>0)经过点A,交AB于点C,且AC=BC,OA=3,则k=3$\sqrt{2}$.
如图,直角△AOB的斜边OB在x轴正半轴上,双曲线y=$\frac{k}{x}$(x>0)经过点A,交AB于点C,且AC=BC,OA=3,则k=3$\sqrt{2}$.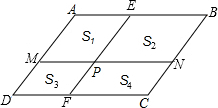 如图,在平行四边形ABCD中.AB∥CD,AD∥BC,P为平行四边形ABCD内一点,过P作EF∥BC,MN∥CD,设四边形AMPE、四边形EPNB、四边形MDFP、四边形CFPN的面积分别为S1、S2、S3、S4.
如图,在平行四边形ABCD中.AB∥CD,AD∥BC,P为平行四边形ABCD内一点,过P作EF∥BC,MN∥CD,设四边形AMPE、四边形EPNB、四边形MDFP、四边形CFPN的面积分别为S1、S2、S3、S4.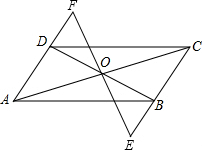 如图,在?ABCD中,对角线AC,BD交于点O,过点O的直线分别交CB,AD的延长线于点E,F,BE与DF相等吗?为什么?
如图,在?ABCD中,对角线AC,BD交于点O,过点O的直线分别交CB,AD的延长线于点E,F,BE与DF相等吗?为什么?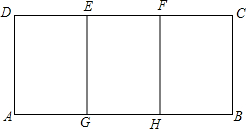 如图,矩形ABCD能分成三个全等的小矩形,且每个小矩形都与矩形ABCD相似,已知AD=1,求AB的长.
如图,矩形ABCD能分成三个全等的小矩形,且每个小矩形都与矩形ABCD相似,已知AD=1,求AB的长.