题目内容
9.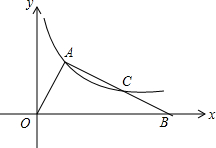 如图,直角△AOB的斜边OB在x轴正半轴上,双曲线y=$\frac{k}{x}$(x>0)经过点A,交AB于点C,且AC=BC,OA=3,则k=3$\sqrt{2}$.
如图,直角△AOB的斜边OB在x轴正半轴上,双曲线y=$\frac{k}{x}$(x>0)经过点A,交AB于点C,且AC=BC,OA=3,则k=3$\sqrt{2}$.
分析 作AD⊥x轴于D,CE⊥x轴于E,如图,设A(t,$\frac{k}{t}$),先证明CE为△ADB的中位线得到CE=$\frac{1}{2}$AD=$\frac{k}{2t}$,DE=BE,则利用反比例函数图象上点的坐标特征可表示出C(2t,$\frac{k}{2t}$),于是得到DE=BE=t,然后证明△OAD∽△OBA,利用相似比计算出t,再利用勾股定理计算出k.
解答 解:作AD⊥x轴于D,CE⊥x轴于E,如图,
设A(t,$\frac{k}{t}$),
∵CE∥AD,AC=BC,
∴CE=$\frac{1}{2}$AD=$\frac{k}{2t}$,DE=BE,
∴C(2t,$\frac{k}{2t}$),
∴DE=BE=t,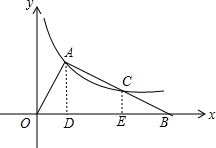
∵∠AOD=∠BOA,
∴△OAD∽△OBA,
∴OA:OB=OD:OA,即3:3t=t:3,解得t=$\sqrt{3}$,
在Rt△OAD中,($\sqrt{3}$)2+($\frac{k}{\sqrt{3}}$)2=32,
∴k=3$\sqrt{2}$.
故答案为3$\sqrt{2}$.
点评 本题考查了反比例好图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.解决本题的关键是确定OB与OD的关系.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
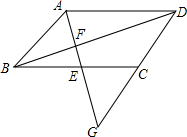 如图,直线AG过平行四边形ABCD的边BC的中点F、交对角线BD于点F,交DC的延长线于G.
如图,直线AG过平行四边形ABCD的边BC的中点F、交对角线BD于点F,交DC的延长线于G.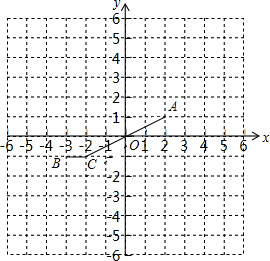 若A、B、C、D四点构成平行四边形A(2,1)、B(-3,1)、C(-2,-1),则顶点D的坐标为(3,1)或(1,1)或(-5,-3).
若A、B、C、D四点构成平行四边形A(2,1)、B(-3,1)、C(-2,-1),则顶点D的坐标为(3,1)或(1,1)或(-5,-3).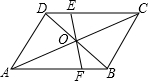 如图,O为?ABCD的对角线的交点,过O点作直线EF分别交CD,AB于点E,F.
如图,O为?ABCD的对角线的交点,过O点作直线EF分别交CD,AB于点E,F.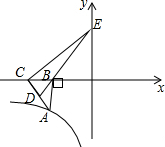 如图,Rt△ABC的直角边BC在x轴负半轴上,斜边AC上的中线BD的反向延长线交y轴正半轴于点E,双曲线y=$\frac{k}{x}$(x<0)的图象经过点A,S△BEC=8,则k=16.
如图,Rt△ABC的直角边BC在x轴负半轴上,斜边AC上的中线BD的反向延长线交y轴正半轴于点E,双曲线y=$\frac{k}{x}$(x<0)的图象经过点A,S△BEC=8,则k=16.
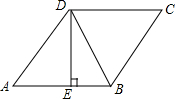 如图,在菱形ABCD中,已知DE⊥AB,AE:AD=3:5,BE=2,则菱形ABCD的面积是20.
如图,在菱形ABCD中,已知DE⊥AB,AE:AD=3:5,BE=2,则菱形ABCD的面积是20.