题目内容
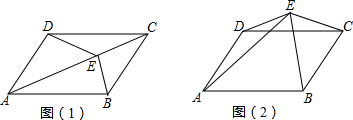
11．
已知：如图，在?ABCD中，E是AB的中点，ED=EC，求证：四边形ABCD是矩形．
分析 根据平行四边形的两组对边分别相等可知△ADE≌△BCE，可知∠A=∠B=90°，所以是矩形．
解答 证明：∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，
∴∠A+∠B=180°，
∵在△ADE和△BCE中，
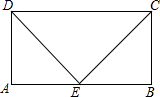
$\left\{\begin{array}{l}{AD=BC}\\{AE=BE}\\{ED=EC}\end{array}\right.$，
∴△ADE≌△BCE（SSS），
∴∠A=∠B=90°，
即可得出平行四边形ABCD是矩形．
点评 此题主要考查了矩形的判定，即有一个角是90度的平行四边形是矩形．
练习册系列答案
相关题目
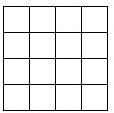如图，将3枚相同硬币依次放入一个4×4的正方形格子中（每个正方形格子只能放1枚硬币）．求所放的3枚硬币中，任意两个都不同行且不同列的概率．
如图，己知△ABC是等腰直角三角形，AC=BC，∠ACB=90°，AE⊥EF于E，BF⊥EF于F，求证：EF=AE+BF．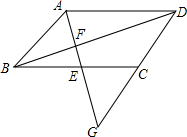
如图，直线AG过平行四边形ABCD的边BC的中点F、交对角线BD于点F，交DC的延长线于G．
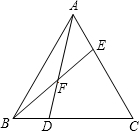如图，已知△ABC中，AE：EC=1：3，BD：DC=1：2，AD与BE交于点F，求$\frac{EF}{BF}$+$\frac{AF}{DF}$的值．
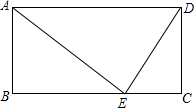已知：如图，在矩形ABCD中，E为BC上一点．若AB=12，AD=25，BE=16，求证：△ABE∽△ECD．
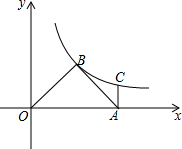如图，△AOB为等腰三角形，∠ABO=90°，点A为x轴上的点，过点A作AC⊥x轴交双曲线y=$\frac{k}{x}$于C，AC=1，求k的值．
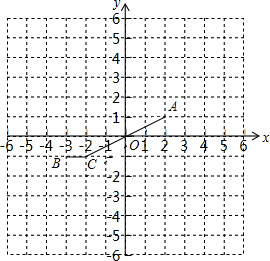若A、B、C、D四点构成平行四边形A（2，1）、B（-3，1）、C（-2，-1），则顶点D的坐标为（3，1）或（1，1）或（-5，-3）．