题目内容
13.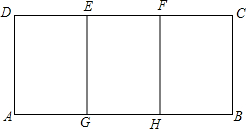 如图,矩形ABCD能分成三个全等的小矩形,且每个小矩形都与矩形ABCD相似,已知AD=1,求AB的长.
如图,矩形ABCD能分成三个全等的小矩形,且每个小矩形都与矩形ABCD相似,已知AD=1,求AB的长.
分析 根据全等图形的性质得到DE=$\frac{1}{3}$DC,根据相似多边形的性质列出比例式,计算即可.
解答 解:∵三个小矩形全等,
∴DE=$\frac{1}{3}$DC,
∵每个小矩形都与矩形ABCD相似,
∴$\frac{AD}{AB}$=$\frac{DE}{AD}$,即$\frac{1}{3}$AB2=1,
解得AB=$\sqrt{3}$.
答:AB的长为$\sqrt{3}$.
点评 本题考查的是相似多边形的性质,掌握相似多边形的性质:①对应角相等;②对应边的比相等是解题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
3.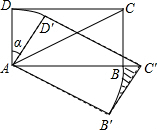 如图,在矩形ABCD中,AB=$\sqrt{3}$,AD=1,把该矩形绕点A顺时针旋转α度得矩形AB′C′D′,点C′落在AB的延长线上,则图中阴影部分的面积是( )
如图,在矩形ABCD中,AB=$\sqrt{3}$,AD=1,把该矩形绕点A顺时针旋转α度得矩形AB′C′D′,点C′落在AB的延长线上,则图中阴影部分的面积是( )
 如图,在矩形ABCD中,AB=$\sqrt{3}$,AD=1,把该矩形绕点A顺时针旋转α度得矩形AB′C′D′,点C′落在AB的延长线上,则图中阴影部分的面积是( )
如图,在矩形ABCD中,AB=$\sqrt{3}$,AD=1,把该矩形绕点A顺时针旋转α度得矩形AB′C′D′,点C′落在AB的延长线上,则图中阴影部分的面积是( )| A. | $\frac{\sqrt{3}}{2}$$-\frac{π}{4}$ | B. | $\frac{\sqrt{3}}{2}-\frac{π}{12}$ | C. | $\frac{\sqrt{3}}{2}-\frac{π}{2}$ | D. | $\frac{\sqrt{3}}{2}-\frac{π}{6}$ |
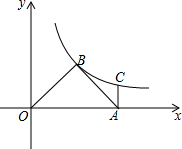 如图,△AOB为等腰三角形,∠ABO=90°,点A为x轴上的点,过点A作AC⊥x轴交双曲线y=$\frac{k}{x}$于C,AC=1,求k的值.
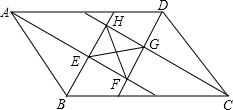
如图,△AOB为等腰三角形,∠ABO=90°,点A为x轴上的点,过点A作AC⊥x轴交双曲线y=$\frac{k}{x}$于C,AC=1,求k的值.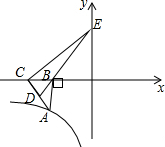 如图,Rt△ABC的直角边BC在x轴负半轴上,斜边AC上的中线BD的反向延长线交y轴正半轴于点E,双曲线y=$\frac{k}{x}$(x<0)的图象经过点A,S△BEC=8,则k=16.
如图,Rt△ABC的直角边BC在x轴负半轴上,斜边AC上的中线BD的反向延长线交y轴正半轴于点E,双曲线y=$\frac{k}{x}$(x<0)的图象经过点A,S△BEC=8,则k=16.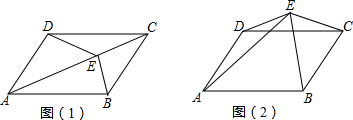
 如图,在?ABCD中,四个内角的平分线分别相交于点E,F,G,H.
如图,在?ABCD中,四个内角的平分线分别相交于点E,F,G,H.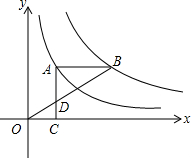 如图,点A在双曲线y=$\frac{2}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AC⊥x轴于C.连接OB与AC相交于点D,若AD=2DC.则k的值为6.
如图,点A在双曲线y=$\frac{2}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AC⊥x轴于C.连接OB与AC相交于点D,若AD=2DC.则k的值为6.