题目内容
6.已知关于x的方程(x+1)2+(x-b)2=2有唯一的实数解,且一次函数y=bx+1的图象在每个象限内y随x的增大而增大,那么一次函数的关系式为( )| A. | y=-3x+1 | B. | y=x+1 | C. | y=2x+1 | D. | y=-2x+1 |
分析 关于x的方程(x+1)2+(x-b)2=2有唯一的实数解,则判别式等于0,据此即可求得b的值,然后根据一次函数y=bx+1的图象在每个象限内y随x的增大而增大,则比例系数b>0,则b的值可以确定,从而确定函数的解析式.
解答 解:关于x的方程(x+1)2+(x-b)2=2化成一般形式是:2x2+(2-2b)x+(b2-1)=0,
△=(2-2b)2-8(b2-1)=-4(b+3)(b-1)=0,
解得:b=-3或1.
∵一次函数y=bx+1的图象在每个象限内y随x的增大而增大,
∴b>0,
∴b=1.
则一次函数的关系式为:y=x+1.
故选B.
点评 本题考查了根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.也考查了一次函数的性质,以及待定系数法求一次函数解析式,正确利用判别式求得b的值是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.化简($\sqrt{3}$-2)200•($\sqrt{3}+2$)201的结果为( )
| A. | -1 | B. | $\sqrt{3}$-2 | C. | $\sqrt{3}$+2 | D. | -$\sqrt{3}$-2 |
14.下列方程是关于x的一元二次方程的是( )
| A. | (x+1)2=x+1 | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$+2=0 | C. | $\sqrt{{x}^{2}-1}$=0 | D. | x2+2x=x2-1 |
1.若abc≠0,且a,b,c满足方程组$\left\{{\begin{array}{l}{5a+2b-9c=0}\\{4a-3b+2c=0}\end{array}}\right.$,则$\frac{5a-b+7c}{3a+2b+3c}$=( )
| A. | -1 | B. | 1 | C. | $-\frac{11}{8}$ | D. | $\frac{11}{8}$ |
18.如果(x2-mx-n)(x-3)的乘积中不含x2项和x项,那么( )
| A. | m=0,n=0 | B. | m=-3,n=-9 | C. | m=-3,n=9 | D. | m=3,n=-9 |
15.设ab≠0,a2+b2=1,如果x=$\frac{{a}^{4}+{b}^{4}}{{a}^{6}+{b}^{6}}$,y=$\frac{{a}^{4}+{b}^{4}}{\sqrt{{a}^{4}+{b}^{4}}}$,z=$\frac{\sqrt{{a}^{4}+{b}^{4}}}{{a}^{6}+{b}^{6}}$,那么x,y,z的大小关系是( )
| A. | x<y<z | B. | y<z<x | C. | z<x<y | D. | y<x<z |
10.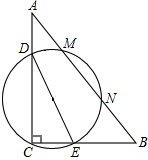 如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
 如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )| A. | $\frac{8}{5}$ | B. | 2 | C. | $\frac{12}{5}$ | D. | $\frac{14}{5}$ |
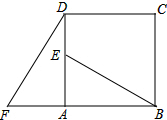 如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如果AF=4,AB=7.
如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如果AF=4,AB=7.