题目内容
19.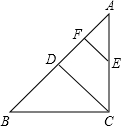 如图,Rt△ABC中,∠ACB=90°,AB=6,点D是AB的中点,过AC的中点E作EF∥CD交AB于点F,则EF=1.5.
如图,Rt△ABC中,∠ACB=90°,AB=6,点D是AB的中点,过AC的中点E作EF∥CD交AB于点F,则EF=1.5.
分析 由直角三角形的性质求出CD=3,中由三角形中位线定理得出EF的长即可.
解答 解:∵Rt△ABC中,∠ACB=90°,AB=6,点D是AB的中点,
∴CD=$\frac{1}{2}$AB=3,
∵过AC的中点E作EF∥CD交AB于点F,
∴EF是△ACD的中位线,
∴EF=$\frac{1}{2}$CD=1.5;
故答案为:1.5.
点评 本题考查了直角三角形斜边上的中线性质、三角形中位线定理,熟练掌握直角三角形的性质和三角形中位线定理是关键.

练习册系列答案
相关题目
14.在△ABC中,∠C=90°,BC=3,AB=5,点D在△ABC的边上,且AD=1,将△ABC折叠,使点B落在点D处,折痕交边AB于点E,交另一边于点F,则BE=2或$\frac{15}{7}$.
11.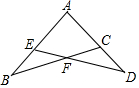 如图,△ABC、△ADE中,C、E两点分别在AD、AB上,且BC与DE相交于F点,若∠A=90°,∠B=∠D=30°,AC=AE=1,则四边形AEFC的周长为何( )
如图,△ABC、△ADE中,C、E两点分别在AD、AB上,且BC与DE相交于F点,若∠A=90°,∠B=∠D=30°,AC=AE=1,则四边形AEFC的周长为何( )
 如图,△ABC、△ADE中,C、E两点分别在AD、AB上,且BC与DE相交于F点,若∠A=90°,∠B=∠D=30°,AC=AE=1,则四边形AEFC的周长为何( )
如图,△ABC、△ADE中,C、E两点分别在AD、AB上,且BC与DE相交于F点,若∠A=90°,∠B=∠D=30°,AC=AE=1,则四边形AEFC的周长为何( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 2+$\sqrt{2}$ | D. | 2+$\sqrt{3}$ |
 如图,AC⊥BC,AD⊥BD,垂足分别是C、D,若要用“HL”得到Rt△ABC≌Rt△BAD,则你添加的条件是AC=BD.(写一种即可)
如图,AC⊥BC,AD⊥BD,垂足分别是C、D,若要用“HL”得到Rt△ABC≌Rt△BAD,则你添加的条件是AC=BD.(写一种即可)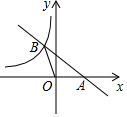 如图,直线y=-$\frac{1}{2}$x+b与x轴交于点A,与双曲线y=-$\frac{4}{x}$(x<0)交于点B,若S△AOB=2,则b的值是( )
如图,直线y=-$\frac{1}{2}$x+b与x轴交于点A,与双曲线y=-$\frac{4}{x}$(x<0)交于点B,若S△AOB=2,则b的值是( )