题目内容
7.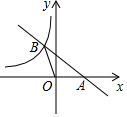 如图,直线y=-$\frac{1}{2}$x+b与x轴交于点A,与双曲线y=-$\frac{4}{x}$(x<0)交于点B,若S△AOB=2,则b的值是( )
如图,直线y=-$\frac{1}{2}$x+b与x轴交于点A,与双曲线y=-$\frac{4}{x}$(x<0)交于点B,若S△AOB=2,则b的值是( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 令y=0代入y=-$\frac{1}{2}$x+b,可求出A(2b,0),由S△AOB=2,可求出B的坐标为$\frac{2}{b}$,从而可求出B的坐标为(-2b,$\frac{2}{b}$),将B(-2b,$\frac{2}{b}$)代入y=-$\frac{1}{2}$x+b即可求出b的值.
解答 解:令y=0代入y=-$\frac{1}{2}$x+b,
∴x=2b
∴A(2b,0)
∴OA=2b
过点B作BC⊥x轴于点C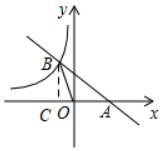
∵S△AOB=2,
∴$\frac{1}{2}$OA•BC=2
∴BC=$\frac{2}{b}$
∴B的坐标为$\frac{2}{b}$
将y=$\frac{2}{b}$代入y=-$\frac{4}{x}$
∴x=-2b
∴B(-2b,$\frac{2}{b}$)
将B(-2b,$\frac{2}{b}$)代入y=-$\frac{1}{2}$x+b
∴$\frac{2}{b}$=2b,
∵b>0
∴b=1
故选(D)
点评 本题考查一次函数的综合问题,解题的关键是根据题意求出点A与B的坐标,本题属于中等题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.在一个不透明袋子中装有5个红球、3个绿球,这些球除了颜色外无其他差别,从袋子中随机摸出一个球,摸出红球的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
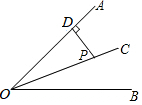 如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,垂足为D,若PD=$\sqrt{3}$,则点P到OB的距离是$\sqrt{3}$.
如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,垂足为D,若PD=$\sqrt{3}$,则点P到OB的距离是$\sqrt{3}$.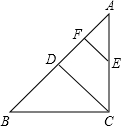 如图,Rt△ABC中,∠ACB=90°,AB=6,点D是AB的中点,过AC的中点E作EF∥CD交AB于点F,则EF=1.5.
如图,Rt△ABC中,∠ACB=90°,AB=6,点D是AB的中点,过AC的中点E作EF∥CD交AB于点F,则EF=1.5.