Question

11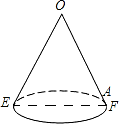．如图是一个底面直径为10，母线OE长也为10的圆锥，A是母线OF上的一点，FA=2，从点E沿圆锥侧面到点A的最短路径长是2$\sqrt{41}$．

Answer 1

分析 要求蚂蚁爬行的最短距离，需将圆锥的侧面展开，求出EA长即可，在Rt△EOA中，OA=8，0E=10，根据勾股定理求出AE，即可得出结果．

解答 解：圆锥侧面沿母线OF展开可得下图：
则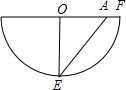$\widehat{EF}$=圆锥底面周长的一半=$\frac{1}{2}$×10π=$\frac{10nπ}{180}$，
∴n=90，即∠EOF=90°，
在Rt△AOE中，OA=8，OE=10，
根据勾股定理可得：AE=2$\sqrt{41}$，
所以蚂蚁爬行的最短距离为2$\sqrt{41}$．
故答案为：2$\sqrt{41}$．

点评 本题考查了圆锥的计算的知识，圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥的母线长．本题就是把圆锥的侧面展开成扇形，“化曲面为平面”，用勾股定理解决．