题目内容
16. 如图,反比例函数y=$\frac{4}{x}$的图象与一次函数y=kx-3的图象在第一象限内相交于点A,且点A的横坐标为4.
如图,反比例函数y=$\frac{4}{x}$的图象与一次函数y=kx-3的图象在第一象限内相交于点A,且点A的横坐标为4.(1)求点A的坐标及一次函数的解析式;
(2)若直线x=2与反比例函数和一次函数的图象分别交于点B、C,求线段BC的长.
分析 (1)由已知先求出m,得出点A的坐标,再把A的坐标代入一次函数y=kx-3求出k的值即可求出一次函数的解析式.
(2)把x=2代入y=$\frac{4}{x}$和y=x-3,得出点B和点C的纵坐标,即可求出线段BC的长.
解答 解:(1)∵点A (4,m)在反比例函数y=$\frac{4}{x}$的图象上,
∴m=$\frac{4}{4}$=1,
∴A(4,1),
把A(4,1)代入一次函数y=kx-3,得4k-3=1,
∴k=1,
∴一次函数的解析式为y=x-3;
(2)∵直线x=2与反比例和一次函数的图象分别交于点B、C,
∴当x=2时,yB=$\frac{4}{2}$=2,
yC=2-3=-1,
∴线段BC的长为|yB-yC|=2-(-1)=3.
点评 此题考查的知识点是反比例函数综合应用,解决本题的关键是利用反比例函数求得关键点点A的坐标,然后利用待定系数法即可求出函数的解析式.

练习册系列答案
相关题目
6.对于函数y=-2x+1有以下四个结论,其中正确的结论是( )
| A. | 函数图象必经过点(-2,1) | B. | 函数图象经过第一、二、三象限 | ||
| C. | 函数值y随x的增大而增大 | D. | 当x>$\frac{1}{2}$,时,y<0 |
7. 如图,教师在小黑板上出示一道题,小华答:过点(3,0);小彬答:过点(4,3);小明答:a=1;小颖答:抛物线被x轴截得的线段长为2.你认为四人的回答中,正确的有( )
如图,教师在小黑板上出示一道题,小华答:过点(3,0);小彬答:过点(4,3);小明答:a=1;小颖答:抛物线被x轴截得的线段长为2.你认为四人的回答中,正确的有( )
 如图,教师在小黑板上出示一道题,小华答:过点(3,0);小彬答:过点(4,3);小明答:a=1;小颖答:抛物线被x轴截得的线段长为2.你认为四人的回答中,正确的有( )
如图,教师在小黑板上出示一道题,小华答:过点(3,0);小彬答:过点(4,3);小明答:a=1;小颖答:抛物线被x轴截得的线段长为2.你认为四人的回答中,正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.关于反比例函数y=$\frac{2}{x}$的图象,下列说法正确的是( )
| A. | 图象经过点(1,1) | |
| B. | 当x<0时,y随x的增大而减小 | |
| C. | 图象的两个分支关于x轴成轴对称 | |
| D. | 图象的两个分支分布在第二、四象限 |
6.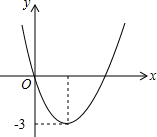 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx=m有两个相等的实数根,则m的值为( )
二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx=m有两个相等的实数根,则m的值为( )
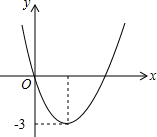 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx=m有两个相等的实数根,则m的值为( )
二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx=m有两个相等的实数根,则m的值为( )| A. | -3 | B. | 3 | C. | -6 | D. | 9 |
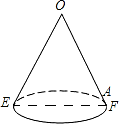 如图是一个底面直径为10,母线OE长也为10的圆锥,A是母线OF上的一点,FA=2,从点E沿圆锥侧面到点A的最短路径长是2$\sqrt{41}$.
如图是一个底面直径为10,母线OE长也为10的圆锥,A是母线OF上的一点,FA=2,从点E沿圆锥侧面到点A的最短路径长是2$\sqrt{41}$.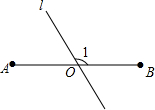 如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP=3或3$\sqrt{3}$或3$\sqrt{7}$.
如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP=3或3$\sqrt{3}$或3$\sqrt{7}$.