题目内容
1. 如图,在△ABC中,E、F分别是AD、CE边的中点,且S△BEF=4cm2,则S△ABC为( )
如图,在△ABC中,E、F分别是AD、CE边的中点,且S△BEF=4cm2,则S△ABC为( )| A. | 1cm2 | B. | 2cm2 | C. | 8cm2 | D. | 16cm2 |
分析 根据三角形的中线把三角形分成两个面积相等的三角形解答.
解答 解:∵点E是AD的中点,
∴S△ABE=$\frac{1}{2}$S△ABD,S△ACE=$\frac{1}{2}$S△ADC,
∴S△ABE+S△ACE=$\frac{1}{2}$S△ABC,
∴S△BCE=$\frac{1}{2}$S△ABC,
∵点F是CE的中点,
∴S△BEF=$\frac{1}{2}$S△BCE.
∴S△ABC=16cm2
故选D
点评 本题考查了三角形的面积,主要利用了三角形的中线把三角形分成两个面积相等的三角形,原理为等底等高的三角形的面积相等.

练习册系列答案
相关题目
9.要判断命题“若a>b,则a2>b2”是假命题,可举得反例是( )
| A. | a=1,b=-2 | B. | a=1,b=0 | C. | a=2,b=1 | D. | a=2,b=-1 |
9.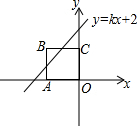 如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x轴的负半轴、y轴的正半轴上.若直线y=kx+2与边AB有公共点,则k的值可能为( )
如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x轴的负半轴、y轴的正半轴上.若直线y=kx+2与边AB有公共点,则k的值可能为( )
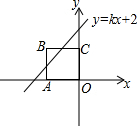 如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x轴的负半轴、y轴的正半轴上.若直线y=kx+2与边AB有公共点,则k的值可能为( )
如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x轴的负半轴、y轴的正半轴上.若直线y=kx+2与边AB有公共点,则k的值可能为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | 3 |
6.对于函数y=-2x+1有以下四个结论,其中正确的结论是( )
| A. | 函数图象必经过点(-2,1) | B. | 函数图象经过第一、二、三象限 | ||
| C. | 函数值y随x的增大而增大 | D. | 当x>$\frac{1}{2}$,时,y<0 |
10.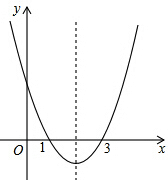 已知二次函数y=ax2+bx+c的图象如图所示,则下列叙述正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列叙述正确的是( )
 已知二次函数y=ax2+bx+c的图象如图所示,则下列叙述正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列叙述正确的是( )| A. | abc<0 | B. | -3a+c<0 | C. | b2-4ac≥0 | D. | 5a+2b+c>0 |
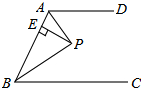 如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=3,则两平行线AD与BC间的距离为( )
如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=3,则两平行线AD与BC间的距离为( )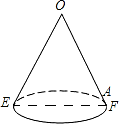 如图是一个底面直径为10,母线OE长也为10的圆锥,A是母线OF上的一点,FA=2,从点E沿圆锥侧面到点A的最短路径长是2$\sqrt{41}$.
如图是一个底面直径为10,母线OE长也为10的圆锥,A是母线OF上的一点,FA=2,从点E沿圆锥侧面到点A的最短路径长是2$\sqrt{41}$.