题目内容
19. 如图,在直角体系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),C是y轴上的点.
如图,在直角体系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),C是y轴上的点.(1)求直线AB的解析式.
(2)求△OAC的面积.
分析 (1)利用待定系数法即可求得直线AB的解析式;
(2)首先求得C的坐标,然后利用三角形的面积公式即可求解.
解答 解:(1)设直线AB的解析式是y=kx+b,
根据题意得:$\left\{\begin{array}{l}{4k+b=2}\\{6k+b=0}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=-1}\\{b=6}\end{array}\right.$,
则直线的解析式是:y=-x+6;
(2)在y=-x+6中,令x=0,解得:y=6,
S△OAC=$\frac{1}{2}$×6×4=12;
点评 本题考查了一次函数关系式为:y=kx+b(k≠0),要有两组对应量确定解析式,即得到k,b的二元一次方程组.

练习册系列答案
相关题目
9.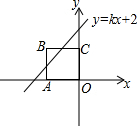 如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x轴的负半轴、y轴的正半轴上.若直线y=kx+2与边AB有公共点,则k的值可能为( )
如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x轴的负半轴、y轴的正半轴上.若直线y=kx+2与边AB有公共点,则k的值可能为( )
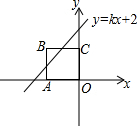 如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x轴的负半轴、y轴的正半轴上.若直线y=kx+2与边AB有公共点,则k的值可能为( )
如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x轴的负半轴、y轴的正半轴上.若直线y=kx+2与边AB有公共点,则k的值可能为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | 3 |
10.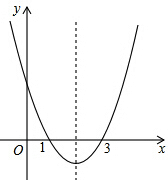 已知二次函数y=ax2+bx+c的图象如图所示,则下列叙述正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列叙述正确的是( )
 已知二次函数y=ax2+bx+c的图象如图所示,则下列叙述正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列叙述正确的是( )| A. | abc<0 | B. | -3a+c<0 | C. | b2-4ac≥0 | D. | 5a+2b+c>0 |
7. 如图,教师在小黑板上出示一道题,小华答:过点(3,0);小彬答:过点(4,3);小明答:a=1;小颖答:抛物线被x轴截得的线段长为2.你认为四人的回答中,正确的有( )
如图,教师在小黑板上出示一道题,小华答:过点(3,0);小彬答:过点(4,3);小明答:a=1;小颖答:抛物线被x轴截得的线段长为2.你认为四人的回答中,正确的有( )
 如图,教师在小黑板上出示一道题,小华答:过点(3,0);小彬答:过点(4,3);小明答:a=1;小颖答:抛物线被x轴截得的线段长为2.你认为四人的回答中,正确的有( )
如图,教师在小黑板上出示一道题,小华答:过点(3,0);小彬答:过点(4,3);小明答:a=1;小颖答:抛物线被x轴截得的线段长为2.你认为四人的回答中,正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.直线y1=2x+2关于x轴对称的直线为y2,则当y1>y2时,自变量x的取值范围是( )
| A. | x>-1 | B. | x<-1 | C. | x>2 | D. | x>0 |
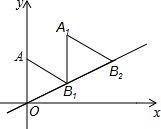 如图放置的△OAB1,△B1A1B2都是边长为2的等边三角形,边AO在y轴上,点B1,B2都在直线y=$\frac{\sqrt{3}}{3}$x上,则点B2的坐标为(2$\sqrt{3}$,2).
如图放置的△OAB1,△B1A1B2都是边长为2的等边三角形,边AO在y轴上,点B1,B2都在直线y=$\frac{\sqrt{3}}{3}$x上,则点B2的坐标为(2$\sqrt{3}$,2).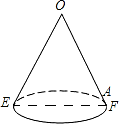 如图是一个底面直径为10,母线OE长也为10的圆锥,A是母线OF上的一点,FA=2,从点E沿圆锥侧面到点A的最短路径长是2$\sqrt{41}$.
如图是一个底面直径为10,母线OE长也为10的圆锥,A是母线OF上的一点,FA=2,从点E沿圆锥侧面到点A的最短路径长是2$\sqrt{41}$.