题目内容
5.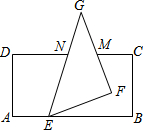 如图,将一张长方形纸片与一张直角三角形纸片(∠EFG=90°)按如图所示的位置摆放,使直角三角形纸片的一个顶点E恰好落在长方形纸片的一边AB上,已知∠BEF=21°,则∠CMF=69°.
如图,将一张长方形纸片与一张直角三角形纸片(∠EFG=90°)按如图所示的位置摆放,使直角三角形纸片的一个顶点E恰好落在长方形纸片的一边AB上,已知∠BEF=21°,则∠CMF=69°.
分析 先延长MF交AB于H,得出∠EFG=90°,再根据三角形外角性质,求得∠BHF的度数,最后根据平行线的性质,求得∠CMF的度数.
解答  解:延长MF交AB于H,则∠EFG=90°
解:延长MF交AB于H,则∠EFG=90°
∵∠BEF=21°
∴∠BHF=90°+21°=111°
∵CD∥AB
∴∠CNF=180°-∠BHF=180°-111°=69°
故答案为:69°
点评 本题主要考查了平行线的性质,三角形的外角性质,解决问题的关键是作辅助线构造直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.若abc≠0,且a,b,c满足方程组$\left\{{\begin{array}{l}{5a+2b-9c=0}\\{4a-3b+2c=0}\end{array}}\right.$,则$\frac{5a-b+7c}{3a+2b+3c}$=( )
| A. | -1 | B. | 1 | C. | $-\frac{11}{8}$ | D. | $\frac{11}{8}$ |
10.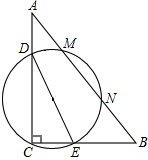 如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
 如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )| A. | $\frac{8}{5}$ | B. | 2 | C. | $\frac{12}{5}$ | D. | $\frac{14}{5}$ |
17.若关于x的不等式3x<a+5与2x<4的解集相同,则a的值是( )
| A. | 1 | B. | 7 | C. | 2 | D. | 5 |

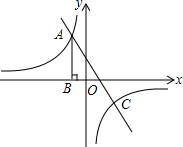 如图,反比例函数y=$\frac{k}{x}$的图象经过第二象限内的点A,AB⊥x轴于点B,OB=1,AB=4.
如图,反比例函数y=$\frac{k}{x}$的图象经过第二象限内的点A,AB⊥x轴于点B,OB=1,AB=4.