题目内容
15.已知二次函数y=x2-2ax在x≥2时,函数y随着x的增大而增大,则实数a的取值范围是a≤2.分析 把二次函数解析式化为顶点式,可求得其对称轴,由条件可判断出对称轴和x=2的关系,从而可得到关于a的不等式,可求得a的取值范围.
解答 解:
∵y=x2-2ax=(x-a)2-a2,
∴二次函数开口向上,对称轴为直线x=a,
当x<a时,y随x的增大而减小,当x≥a时,y随x的增大而增大,
∵在x≥2时,函数y随着x的增大而增大,
∴二次函数的对称轴在直线x=2的左侧,
∴a≤2,
故答案为:a≤2.
点评 本题主要考查二次函数的性质,掌握二次函数的增减性是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.若$\sqrt{5}$的值为a,则a的范围为( )
| A. | 1<a<2 | B. | 2<a<3 | C. | 3<a<4 | D. | 4<a<5 |
3. 将一个三角形和一个矩形按照如图的方式扩大,使他们的对应边之间的距离均为1,得到新的三角形和矩形,下列说法正确的是( )
将一个三角形和一个矩形按照如图的方式扩大,使他们的对应边之间的距离均为1,得到新的三角形和矩形,下列说法正确的是( )
 将一个三角形和一个矩形按照如图的方式扩大,使他们的对应边之间的距离均为1,得到新的三角形和矩形,下列说法正确的是( )
将一个三角形和一个矩形按照如图的方式扩大,使他们的对应边之间的距离均为1,得到新的三角形和矩形,下列说法正确的是( )| A. | 新三角形与原三角形相似 | |
| B. | 新矩形与原矩形相似 | |
| C. | 新三角形与原三角形、新矩形与原矩形都相似 | |
| D. | 新三角形与原三角形、新矩形与原矩形都不相似 |
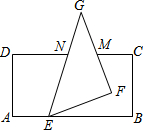 如图,将一张长方形纸片与一张直角三角形纸片(∠EFG=90°)按如图所示的位置摆放,使直角三角形纸片的一个顶点E恰好落在长方形纸片的一边AB上,已知∠BEF=21°,则∠CMF=69°.
如图,将一张长方形纸片与一张直角三角形纸片(∠EFG=90°)按如图所示的位置摆放,使直角三角形纸片的一个顶点E恰好落在长方形纸片的一边AB上,已知∠BEF=21°,则∠CMF=69°. 如图,在平面直角坐标系中,等腰直角三角形AOB的直角顶点A在第四象限,顶点B(0,-2),点C(0,1),点D在边AB上,连接CD交OA于点E,反比例函数$y=\frac{k}{x}$的图象经过点D,若△ADE和△OCE的面积相等,则k的值为-$\frac{8}{9}$.
如图,在平面直角坐标系中,等腰直角三角形AOB的直角顶点A在第四象限,顶点B(0,-2),点C(0,1),点D在边AB上,连接CD交OA于点E,反比例函数$y=\frac{k}{x}$的图象经过点D,若△ADE和△OCE的面积相等,则k的值为-$\frac{8}{9}$.