题目内容
13.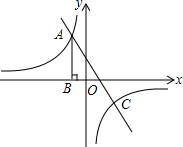 如图,反比例函数y=$\frac{k}{x}$的图象经过第二象限内的点A,AB⊥x轴于点B,OB=1,AB=4.
如图,反比例函数y=$\frac{k}{x}$的图象经过第二象限内的点A,AB⊥x轴于点B,OB=1,AB=4.(1)求k的值;
(2)若直线y=ax+b经过点A,并且经过反比例函数y=$\frac{k}{x}$的图象上另一点C(n,-2),求直线y=ax+b的解析式.
分析 (1)根据题意易得点A的坐标为(-1,4),将其代入函数解析式即可求得k的值;
(2)利用反比例函数图象上点的坐标特点求得点C的坐标,然后结合点A、C的坐标来求直线方程即可.
解答 解:(1)∵OB=1,AB=4,
∴A(-1,4),
∵反比例函数y=$\frac{k}{x}$的图象经过第二象限内的点A,
∴k=xy=-4;
(2)∵反比例函数y=-$\frac{4}{x}$的图象经过点C(n,-2),
∴-2=-$\frac{4}{n}$,
解得n=2,
∴C(2,-2),
∵直线y=ax+b经过点A,C,
∴$\left\{\begin{array}{l}{-a+b=4}\\{2a+b=-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-2}\\{b=2}\end{array}\right.$,
则该直线方程为:y=-2x+2.
点评 本题考查了反比例函数与一次函数交点问题.解题时,需要掌握函数图象上点的坐标特征.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
10. 如图,分别以五边形ABCDE的顶点为圆心,以1为半径作五个圆,则图中阴影部分的面积之和为( )
如图,分别以五边形ABCDE的顶点为圆心,以1为半径作五个圆,则图中阴影部分的面积之和为( )
 如图,分别以五边形ABCDE的顶点为圆心,以1为半径作五个圆,则图中阴影部分的面积之和为( )
如图,分别以五边形ABCDE的顶点为圆心,以1为半径作五个圆,则图中阴影部分的面积之和为( )| A. | $\frac{3}{2}π$ | B. | 3π | C. | $\frac{7}{2}π$ | D. | 2π |
1.某商场购进商品后,加价40%作为销售价.商场搞优惠促销,决定由顾客抽奖确定折扣.某顾客购买甲、乙两种商品,分别抽到七折和九折,共付款399元,两种商品原售价之和为490元,甲、乙两种商品的进价分别是( )
| A. | 200元,150元 | B. | 210元,280元 | C. | 280元,210元 | D. | 150元,200元 |
3. 将一个三角形和一个矩形按照如图的方式扩大,使他们的对应边之间的距离均为1,得到新的三角形和矩形,下列说法正确的是( )
将一个三角形和一个矩形按照如图的方式扩大,使他们的对应边之间的距离均为1,得到新的三角形和矩形,下列说法正确的是( )
 将一个三角形和一个矩形按照如图的方式扩大,使他们的对应边之间的距离均为1,得到新的三角形和矩形,下列说法正确的是( )
将一个三角形和一个矩形按照如图的方式扩大,使他们的对应边之间的距离均为1,得到新的三角形和矩形,下列说法正确的是( )| A. | 新三角形与原三角形相似 | |
| B. | 新矩形与原矩形相似 | |
| C. | 新三角形与原三角形、新矩形与原矩形都相似 | |
| D. | 新三角形与原三角形、新矩形与原矩形都不相似 |
 解不等式组,并把解集在数轴上表示出来
解不等式组,并把解集在数轴上表示出来 如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.
如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E. 如图,从y=ax2的图象上可以看出,当-1≤x≤2时,y的取值范围是0≤y≤4.
如图,从y=ax2的图象上可以看出,当-1≤x≤2时,y的取值范围是0≤y≤4. 如图,将一张长方形纸片与一张直角三角形纸片(∠EFG=90°)按如图所示的位置摆放,使直角三角形纸片的一个顶点E恰好落在长方形纸片的一边AB上,已知∠BEF=21°,则∠CMF=69°.
如图,将一张长方形纸片与一张直角三角形纸片(∠EFG=90°)按如图所示的位置摆放,使直角三角形纸片的一个顶点E恰好落在长方形纸片的一边AB上,已知∠BEF=21°,则∠CMF=69°.