题目内容

12．函数y=12+4x-x2的图象与x轴有2个交点，当x＜2时，y值随x值增大而增大，当x=2时，y有最大值．

分析 判定方程的判别式即可得到图象与x轴交点的个数；求出抛物线对称轴即可得到y随x的增大而增大时自变量x的取值范围；利用公式法或配方法即可求出函数的最值．

解答 解：
∵y=-x2+4x+12对应方程为0=-x2+4x+12，
∴△=b2-4ac=64＞0，
∴函数y=12+4x-x2的图象与x轴有2个交点；
∵y=-x2+4x+12=-（x-2）2+16，
∴当x＜2时，y值随x值增大而增大，当x=2时，y有最大值．
故答案为：2；x＜2，大．

点评 本题考查了二次函数的有关性质，得出二次函数对称轴再利用函数图象得出x的取值范围是解题关键．

练习册系列答案
相关题目
2．若3x-2nym与xmy-3n的积与$\frac{1}{2}$x4y3是同类项，则m+2n的立方根（　　）
A．-2B．2C．±2D．8
3．请选择一组你喜欢的a、b、c的值，使二次函数y=ax2+bx+c（a≠0）的图象同时满足下列条件：
①开口向下
②当x≤2时，y随x的增大而增大；当x≥2时，y随x的增大而减小．
这样的二次函数的解析式可以是y=-x2+4x+1答案不唯一．
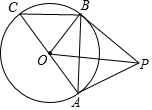20．如图，已知AC是⊙O的直径，BC是⊙O的弦，P是⊙O外一点，连接PB，AB，OB，且∠PBA=∠ACB．
（1）求证：PB是⊙O的切线；
（2）连接OP，若AP=BP，且OP=8，⊙O的半径是2$\sqrt{2}$，求△OAP的面积．
7．已知3m=4，3m-4n=$\frac{4}{81}$，求2013n的值．
17．如图，直线l1∥l2∥l3，直线AC分别交l1、l2、l3于A、B、C，直线DF分别交l1、l2、l3于D、E、F，AC交DF于H，若AH=2，HB=1，BC=5，则$\frac{DE}{EF}$的值为$\frac{3}{5}$，$\frac{DH}{HF}$的值为$\frac{1}{3}$．
4．将下列各式因式分解：
（1）a4-16
（2）16（a-b）2-9（a+b）2
（3）（x+y）2+2（x+y）+1
（4）（m+n）2-2（m2-n2）+（m-n）2．
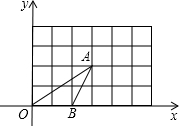1．如图，△OAB的顶点坐标分别为O（0，0）、A（3，2）、B（2，0），将这三个顶点的坐标同时扩大到原来的2倍，得到对应点D、E、F．
（1）在图中画出△DEF；
（2）点E是否在直线OA上？为什么？
（3）△OAB与△DEF是位似图形（填“是”或“不是”）
14．已知有理数a、b在数轴上的位置如图，则比较a、b、-a、-b的大小为a＜-b＜b＜-a．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网