题目内容
2.若3x-2nym与xmy-3n的积与$\frac{1}{2}$x4y3是同类项,则m+2n的立方根( )| A. | -2 | B. | 2 | C. | ±2 | D. | 8 |
分析 先依据单项式乘单项式法则计算,然后依据同类项的定义得到关于m、n的方程组,于是可求得m、n的值,然后再求得m+2n的值,最后求立方根即可.
解答 解:3x-2nym•xmy-3n=3xm-2nym-3n.
∵3x-2nym与xmy-3n的积与($\frac{1}{2}$)4y3是同类项,
∴m-2n=4,m-3n=3,
解得n=1,m=6.
∴m+2n=8.
∴m+2n的立方根为2.
故选:B.
点评 本题主要考查的是单项式乘单项式,熟练掌握相关法则是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.民谚有云:“不到庐山辜负目,不食螃蟹辜负腹.”,又到了食蟹的好季节啦!某经销商去水产批发市场采购太湖蟹,他看中了A、B两家的某种品质相近的太湖蟹.零售价都为120元/千克,批发价各不相同.
A家规定:当批发数量不超过100千克时,所购蟹均按零售价的92%优惠;当批发数量超过100千克但不超过200千克时,所购蟹均按零售价的90%优惠;当批发量超过200千克时,所购蟹均按零售价的88%优惠.
B家的规定如下表:
(1)如果他批发80千克太湖蟹,则他在A 家批发需要8832元,在B家批发需要8760 元;
(2)如果他批发x千克太湖蟹 (150<x<200),则他在A 家批发需要108x元,在B家批发需要90x+2400元(用含x的代数式表示);
(3)现在他要批发180千克太湖蟹,你能帮助他选择在哪家批发更优惠吗?请说明理由.
A家规定:当批发数量不超过100千克时,所购蟹均按零售价的92%优惠;当批发数量超过100千克但不超过200千克时,所购蟹均按零售价的90%优惠;当批发量超过200千克时,所购蟹均按零售价的88%优惠.
B家的规定如下表:
| 数量范围 (千克) | 0~50部分 (含50) | 50以上~150部分(含150,不含50) | 150以上~250部分(含250,不含150) | 250以上部分 (不含250) |
| 价 格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
(2)如果他批发x千克太湖蟹 (150<x<200),则他在A 家批发需要108x元,在B家批发需要90x+2400元(用含x的代数式表示);
(3)现在他要批发180千克太湖蟹,你能帮助他选择在哪家批发更优惠吗?请说明理由.
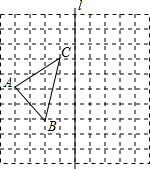 如图,网格中每个小正方形的边长都为1,
如图,网格中每个小正方形的边长都为1,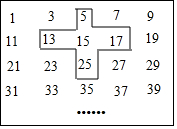 如图是由1,3,5,7,9,…按一定的规律列成的方阵,红十字图案按如图所示的方式框出5个数.
如图是由1,3,5,7,9,…按一定的规律列成的方阵,红十字图案按如图所示的方式框出5个数.