题目内容
2.关于x的不等式|x-3|≤|x+a|的解包含了不等式x≥a,求实数a的取值范围.分析 不等式|x+a|≥|x-3|两边平方,以便去掉绝对值,利用不等式的性质进行讨论.
解答 解:原不等式等价于(x+a)2≥(x-3)2,即x(a+3)≥(a+3)$\frac{3-a}{2}$,
当a=-3时,x取任意实数,a=-3符合要求;
当a>-3时,x≥$\frac{3-a}{2}$,令a≥$\frac{3-a}{2}$得,a≥1;
当a<-3时,x≤$\frac{3-a}{2}$,无解,
因此,a的取值范围是a≥1或a=-3.
点评 本题主要考查绝对值不等式的求解,根据题意去掉绝对值符号是解题的根本,由不等式的解集分类讨论是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
10.用配方法将方程x2-4x+2=0变形,正确的是( )
| A. | (x-2)2=0 | B. | (x-2)2=2 | C. | (x+2)2=0 | D. | (x+2)2=2 |
 如图,等边三角形ABC内接于⊙O,点P是⊙O上一动点(点P不与点B,C重合),则∠CPB的度数为60°.
如图,等边三角形ABC内接于⊙O,点P是⊙O上一动点(点P不与点B,C重合),则∠CPB的度数为60°.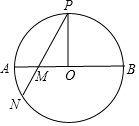 如图,AB是⊙O的直径,PO⊥AB交⊙O于点P,弦PN与AB相交于点M,求证:PM•PN=2PO2.
如图,AB是⊙O的直径,PO⊥AB交⊙O于点P,弦PN与AB相交于点M,求证:PM•PN=2PO2.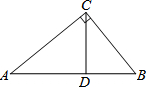 如图所示,△ABC中,∠ACB=90°,CD⊥AB于点D,若BD:AD=1:4,则tan∠BCD=$\frac{1}{2}$.
如图所示,△ABC中,∠ACB=90°,CD⊥AB于点D,若BD:AD=1:4,则tan∠BCD=$\frac{1}{2}$.