题目内容
17.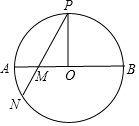 如图,AB是⊙O的直径,PO⊥AB交⊙O于点P,弦PN与AB相交于点M,求证:PM•PN=2PO2.
如图,AB是⊙O的直径,PO⊥AB交⊙O于点P,弦PN与AB相交于点M,求证:PM•PN=2PO2.
分析 延长PO交⊙O于点Q,连接NQ,由PQ为直径且PO⊥AB得∠POM=∠PNQ=90°,根据∠OPM=∠NPQ可证△POM∽△PNQ得$\frac{PM}{PQ}$=$\frac{PO}{PN}$,即PM•PN=PQ•PO=2PO•PO=2PO2.
解答 证明:延长PO交⊙O于点Q,连接NQ,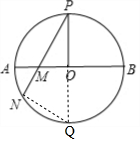
∵PO⊥AB,
∴∠POM=∠PNQ=90°,
∵∠OPM=∠NPQ,
∴△POM∽△PNQ,
∴$\frac{PM}{PQ}$=$\frac{PO}{PN}$,
∵PQ=2PO,
∴PM•PN=PQ•PO=2PO•PO=2PO2,
即PM•PN=2PO2.
点评 本题主要考查圆周角定理、相似三角形的判定与性质,根据直径所对圆周角为直角得出∠POM=∠PNQ=90°,从而证得两三角形相似是解题的关键.

练习册系列答案
相关题目
7.若x>y,则下列式子错误的是( )
| A. | x-2>y-2 | B. | x+1>y+1 | C. | $\frac{x}{5}$>$\frac{y}{5}$ | D. | -5x>-5y |
8.已知关于x的一元二次方程x2+kx+k=0的一根是-2,则另一根x=( )
| A. | -2 | B. | -4 | C. | 2 | D. | 4 |
6.下列一元二次方程中没有实数根的是( )
| A. | (x-1)2=0 | B. | x2+3x+2=0 | C. | x2-4=0 | D. | x2+x+2=0 |
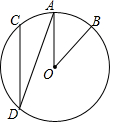 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是20°.
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是20°.